Geradengleichung mit Wertetabelle aufstellen.

Question

Aufgabe:

Geradengleichung durch Tabelle aufstellen.

Problem/Ansatz:

y2-y1/ x2-x1

Reicht dieser Ansatz oder geht es auch einfacher?

Text erkannt:

Aufgabe 5: Fülle die Wertetabellen aus und ermittle jeweils die Geradengleichung.
\begin{tabular}{|l|c|c|c|c|c|c|c|c|c|}
\hline \multicolumn{1}{|c|}{\( \mathrm{X} \)} & \( -4 \) & \( -3 \) & \( -2 \) & \( -1 \) & 0 & 1 & 2 & 3 & 4 \\
\hline \( \mathrm{f}_{1(\mathrm{x})}= \) & & & 2 & & & & 4 & & \\
\hline & & \( -\frac{1}{2} \) & 2 & & & & & & \\
\hline & 9,5 & & & & 1,5 & & & & \\
\hline
\end{tabular}

Answer 1

... oder geht es auch einfacher?

Es geht nur komplizierter: Mach Klammern um den Zähler, und mach Klammern um den Nenner.

Dann hast Du die Steigung, aber noch nicht die Geradengleichung.

Answer 2

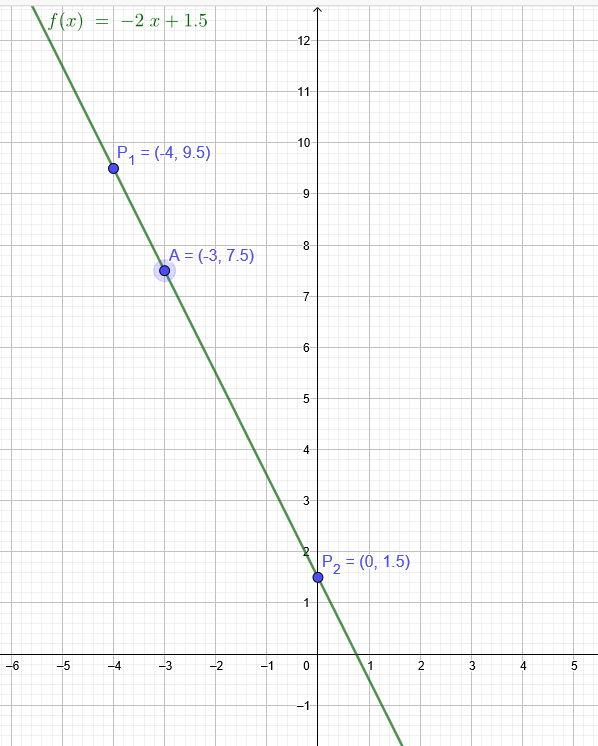
Allgemeine Geradengleichung:

\( \frac{y₂-y₁}{x₂-x₁}= \frac{y-y₁}{x-x₁} \)

 \(y₂=1,5         x₂=0\)
 \(y₁=9,5         x₁=-4\)

\( \frac{1,5-9,5}{0-(-4)}= \frac{y-9,5}{x-(-4)} \)

\( \frac{-8}{4}= \frac{y-9,5}{x+4} \)

\(  \frac{y-9,5}{x+4}=-2 \)

\( y=-2x+1,5 \)

\( f(-3)=-2*(-3)+1,5=7,5\)