a) Paul hat 120 Euro schulden, das bedeutet, dass sein Kontostand bei -120€ liegt.
Paul zahlt jede Woche 15€ zurück -> Jede Woche steigt sein Kontostand um 15€
Das kannst du jetzt als Funktion darstellen. Die -120 nimmst du als y-Achsenabschnitt, da das sozusagen der Startwert ist und als Steigung nimmst du +15x.
Paul
f(x) = -120 + 15x
(Auf der y-Achse wird Pauls Kontostand in € angeben und bei der x-Achse ist 1x = 1 Woche)
Für Melanie dann:
g(x) = 300 - 70x
b) Paul ist schuldenfrei, wenn sein Kontostand nicht mehr negativ ist. Das ist dann der Fall wenn der Graph nicht mehr unter der x-Achse ist, sondern sie schneidet. Gesucht ist also die Nullstelle von f(x) = -120 +15x
Die berechnet man so:
f(x) = 0
0 = -120 + 15x | +120
120 = 15x | :15
8 = x
(Oben haben wir ja bereits erwähnt, dass ein x eine Woche entspricht.)
Als Antwort haben dann:
Paul ist nach 8 Wochen schuldenfrei.
Nun zu Melanie:
Melanie startet mit 300€, das heißt der Graph ihrer Funktion ist über der x-Achse. Und auch hier ist die Nullstelle gesucht, denn das ist die Stelle wo sie kein Geld mehr hat. Rechnung sieht also folgendermaßen aus:
g(x) = 0
0 = 300 - 70x | -300
-300 = -70x | : (-70)
x = 4,2857.....
Da die Zahl mit so viel Nachkommastellen bisschen komisch ist, rechnen wir die 0,2857... am besten in Tage um.
Wir haben also 4 Wochen und 0,2857 * 7 = 2 Tage.
Als Antwort dann:
Melanie hat nach 4 Wochen und 2 Tagen kein Geld mehr.
c) In Geogebra gibt du dann die Gleichungen ein und dann sieht es dann so aus:
Aber hier noch folgender Tipp um dir das in Geogebra besser anzuschauen:
1. Klicke auf das Einstellungsrad oben rechts
2. Dann auf Einstellungen
3. Geeignete Werte für die x und y-Achse eingeben
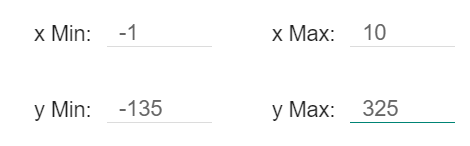
Wenn du die Gleichungen eingetragen hast und dir das Intervall für x und y eingestellt hast, müsstest du dann sowas sehen. Und hier kannst du das mit den Nullstellen nochmal überprüfen. Man sieht ja, dass der grüne Graph (der von Paul) die x-Achse bei 8 schneidet, was wir oben auch ausgerechnet haben. Und, dass der blaue Graph (der von Melanie) die x-Achse bei ungefähr 4,2 schneidet, das kommt also auch hin.
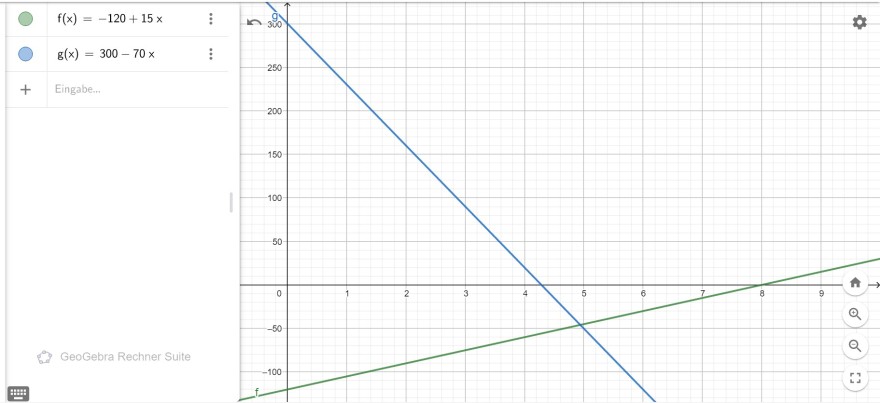
d) In welchem Zeitpunkt sind der Kontostand von Paul und Melanie gleich?
Gesucht ist der Schnittpunkt der beiden Graphen, denn am Schnittpunkt haben beide Graphen den selben y-Wert (= Kontostand).
Um den Schnittpunkt von 2 Funktionen auszurechnen musst du sie gleichsetzen.
Also: f(x) = g(x)
- 120 + 15x = 300 - 70x | + 120
15x = 420 - 70x | +70x
85x = 420 | :85
x = 4,9412
Das kannst du auch in Geogebra an folgender Stelle nochmal kontrollieren:
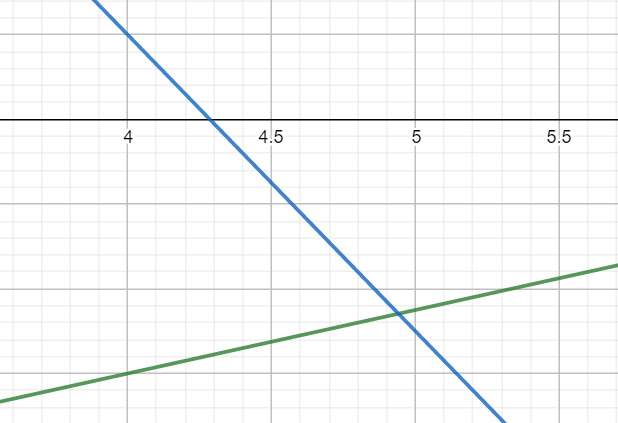
Da es ein bisschen komisch ist zu sagen, dass der Kontostand von Paul und Melanie nach 4,9412 Wochen gleich groß ist, empfehle ich die Nachkommastellen in Tage und Stunden umzurechen:
0,94117647 * 7 = 6,58823529 Tage und bei den Tagen die Nachkommastellen dann in Stunden
0,58823529 * 24 = 14,11764696 Stunden und diese Nachkommastellen dann in Minuten
0,11764698 * 60 = 7,0566176 Minuten, und hier dann die Nachkommastellen in Sekunden
0,566176 * 60 = 3,5290559999 Sekunden.
Dann können wir also sagen, dass Pauls und Melanies Kontostand nach etwa 4 Wochen 6 Tagen 14 Stunden 7 Minuten und 3,5 Sekunden gleich groß ist :)