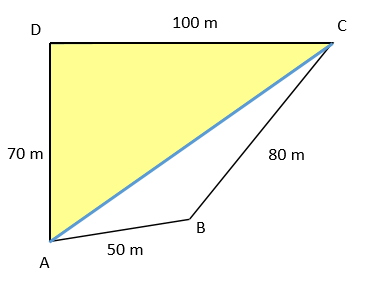
das gelbe Dreieck ist das erste, beim Punkt D hat es einen rechten Winkel. Deswegen lässt sich die Fläche einfach mit A1=100 m * 70 m / 2 = 3500 m² ausrechnen.
Für das zweite Dreieck benötigen wir die Länge der blauen Linie. Mit dem Satz des Pythagoras errechnen wir 122,1 m und erhalten dieses Dreieck.
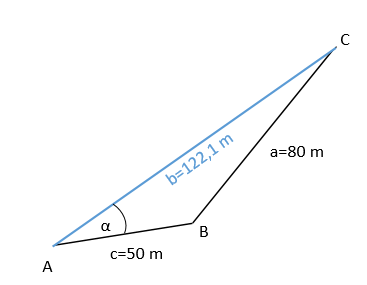
Hier ist die Flächenberechnung schwieriger.
Der Winkel α wird mit dem Kosinussatz errechnet:
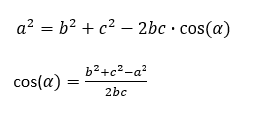
Text erkannt:
\( a^{2}=b^{2}+c^{2}-2 b c \cdot \cos (\alpha) \)
\( \cos (\alpha)=\frac{b^{2}+c^{2}-a^{2}}{2 b c} \)
Es ergibt sich ein Winkel α = 25,7°
α benötigen wir um die Höhe h in diesem zweiten Dreick zu berechnen.
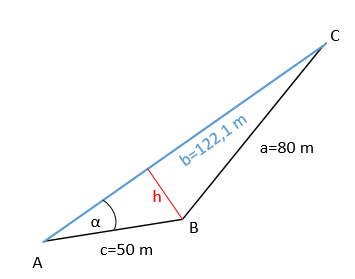
h steht senkrecht auf b und wir sehen ein rechtwinkliges Dreieck. h ist die Gegenkathete und c die Ankathete.
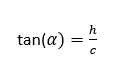
Text erkannt:
\( \tan (\alpha)=\frac{h}{c} \)
eingesetzt erhalten wir h=24,05 m.
Die Fläche eines Dreieckes ist
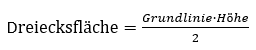
Text erkannt:
Dreiecksfläche \( =\frac{\text { Grundlinie } \cdot \text { Höhe }}{2} \)
Hier ist die Grundline die Strecke b. Damit erhalten wir für dieses zweite Dreieck eine Fläche von
A2=1468 m²
Die Gesamtfläche A=A1+A2 beträgt somit 4968 m²
Durch Auf- und Abrunden könntest du etwas andere Zahlenwerte erhalten. Bei Fragen bitte melden.
Text erkannt:
\( a^{2}=b^{2}+c^{2}-2 b c \cdot \cos (\alpha) \)
\( \cos (\alpha)=\frac{b^{2}+c^{2}-a^{2}}{2 b c} \)
Text erkannt:
\( \alpha \)
