Bestimmen Sie eine Gleichung der Tangente und berechnen Sie die Größe ihres Steigungswinkels.

Question

Aufgabe:

Gegeben sind die Funktion \( f \) und der Punkt P auf dem Graphen \( G_{f} \) von f. Bestimmen Sie eine Gleichung der Tangente an \( \mathrm{G}_{\mathrm{f}} \) in \( \mathrm{P} \) und berechnen Sie die Größe ihres Steigungswinkels.

a) \( f(x)=\sin (x)+x^{2} ; P(0 \mid f(0)) \)
b) \( f(x)=x^{2}-4 x+5 ; P(3 \mid f(3)) \)
c) \( f(x)=2 \cdot \cos (x)-x ; P\left(\frac{\pi}{2} \mid f\left(\frac{\pi}{2}\right)\right) \)

Problem/Ansatz:

Kapiere die Aufgabe nicht. Hoffe jemand kann noch so was. Hat was mit ableiten zu tun

Answer 1

Bestimmen Sie eine Gleichung der Tangente

Die Tangente ist eine Gerade. Du hast von der Geraden einen Punkt (nämlich P) und die Steigung (nämlich die Ableitung von f bei der x-Koordinate von P). Verwende die Punkt-Steigungs-Form.

berechnen Sie die Größe ihres Steigungswinkels.

Das ist der Arcustangens von der Steigung.

Comments

Also man muss einfach irgendeinen zweiten Punkt herausfinden?

Und dann \(\frac{y_2-y_1}{x_2-x_1}\) ?

Hab mit Arcustangens noch nie mit gerechnet

---

Also man muss einfach irgendeinen zweiten Punkt herausfinden?

Nein, das habe ich auch nicht geschrieben. Für die Punkt-Steigungs-Form brauchst Du nur einen Punkt, und die Steigung. Darum heißt sie so.

Hab mit Arcustangens noch nie mit gerechnet

Es gibt immer ein erstes Mal. Dein Taschenrechner kann das.

---

Also man muss einfach irgendeinen zweiten Punkt herausfinden?

Nein - es reicht die Punkt-Steigungsform.

Und dann \(\frac{y_2-y_1}{x_2-x_1}\) ?

Auch nein - die Steigung wird Dir doch durch die Funktion \(f(x)\) gegeben. Wenn $$f(x)= 2\cos(x)-x$$dann ist die Steigung \(f'(x)\)$$f'(x) = -2\sin(x) -1$$und bei \(x=\pi/2\) $$f'\left(\frac{\pi}2\right) = -2\sin\left(\frac{\pi}2\right) - 1 = -3 \\ \arctan(-3) \approx -71,57°$$

---

Dein Taschenrechner kann das.

Den TR legst Du lieber bei Seite (der macht bloss dumm!) Schau Dir lieber diese Antwort an.

Answer 2

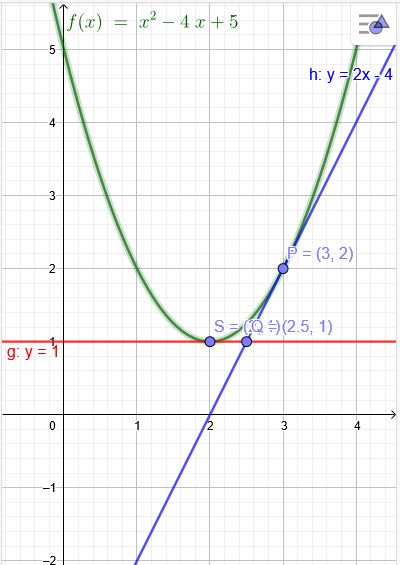
b) \( f(x)=x^{2}-4 x+5 ; P(3 \mid f(3)) \)        \( f(x)=x^{2}-4 x+5 ; P(\blue{3} \mid 2) \)

Scheitelpunkt der Parabel:

\( y=x^{2}-4 x+5\)  → \( y-5=x^{2}-4 x\)    → \( y-5+4=(x-2)^2\)     →                       \( y=(x-2)^2+1\) →

\( S(\red{2}|\orange{1})\)

Die Tangente geht nun durch \( Q(\frac{\red{2}+\blue{3}}{2}|\orange{1})\)  →  \( Q(2,5|1)\)

Tangente:

\( \frac{y-1}{x-2,5}=\frac{2-1}{3-2,5}=\frac{1}{0,5}=2 \)

\( y=2x-4 \)