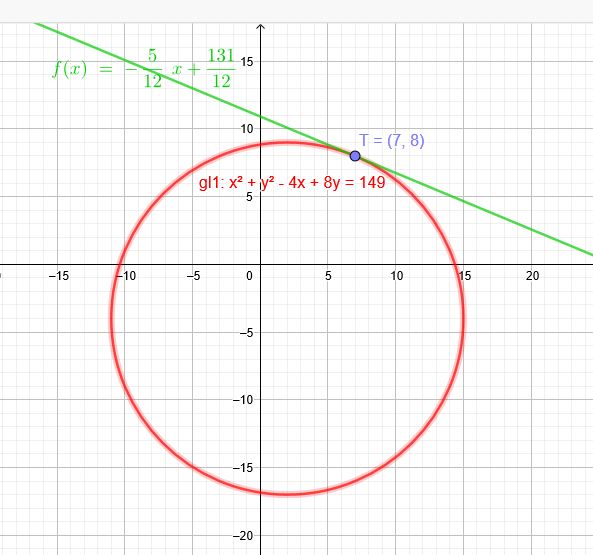
\(f(x,y)= x^2+ y^2-4x+8y-149\)
implizites Differenzieren:
\( \frac{dy}{dx}=-\frac{f_x(x,y)}{f_y(x,y)} \)
\(f_x(x,y)=2x-4\)
\(f_y(x,y)=2y+8\)
\( \frac{dy}{dx}=-\frac{2x-4}{2y+8} =\frac{4-2x}{2y+8}\)
\(T(7|8)\)
\( \frac{dy}{dx}=\frac{4-2*7}{2*8+8}=-\frac{10}{24}=-\frac{5}{12}\)
Tangentengleichung:
\( \frac{y-8}{x-7} =-\frac{5}{12}\)
\(y =-\frac{5}{12}x+\frac{131}{12}\)