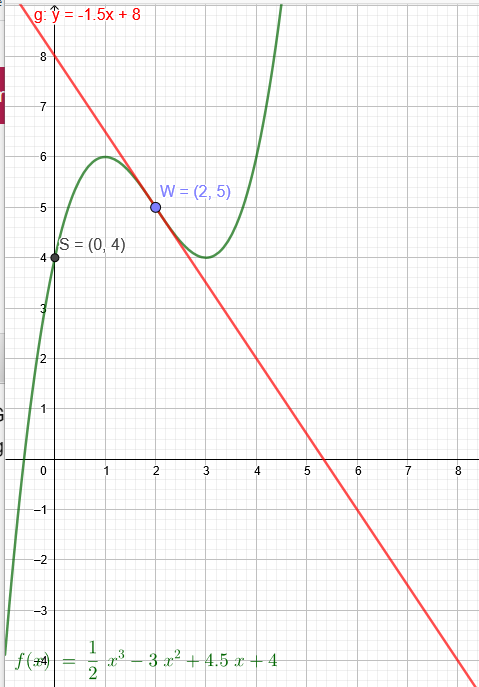
Gesucht wird eine ganzrationale Funktion dritten Grades, deren Graph durch S(0|4) verläuft und in W(2|5) einen Wendepunkt hat. Die Wendetangente hat die Steigung -1,5.
\(f(x)=a*x^3+b*x^2+c*x+d\)
\(S(0|4)\):
\(f(0)=d\)
1.) \(d=4\)
\(W(2|5)\):
\(f(x)=a*x^3+b*x^2+c*x+4\)
\(f(2)=8a+4b+2c+4\)
\(8a+4b+2c+4=5\)
2.) \(8a+4b+2c=1\)
\(f´(x)=3a*x^2+2b*x+c\)
\(f´´(x)=6a*x+2b\)
\(f´´(2)=12a+2b\)
\(12a+2b=0\)
3.) \(b=-6a\)
Wendetangente \(m=-1,5\)
\(f´(2)=12a+4b+c\)
4.) \(12a+4b+c=-1,5\) 4.) \(12a+4*(-6a)+c=-1,5\) 4.) \(c=-1,5+12a\)
2.) \(8a+4b+2c=1\) 2.) \(8a+4*(-6a)+2*(-1,5+12a)=1\)
2.) \(a=0,5\) \(b=-3\) \(c=4,5)\)
\(f(x)=0,5*x^3-3*x^2+4,5x+4\)