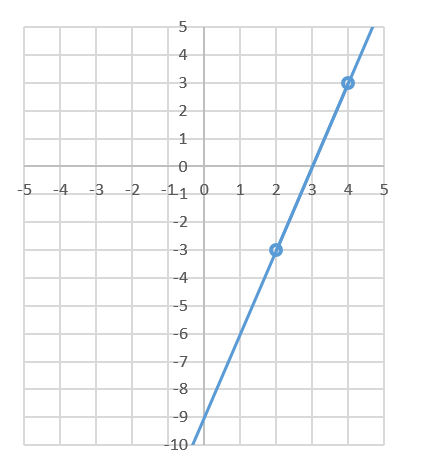
das sind die gegebenen Punkte mit der Geraden dadurch gezeichnet. Du erkennst, dass mit einem Kästchen nach rechts es drei Kästchen nach oben geht. Im Koordinatensystem bedeutet das, wenn x um einen Wert größer wird, wird y um drei Werte größer. Das ergibt eine Steigung von 3. Der Schnittpunkt mit der y-Achse ist -9.
a)
Die Funktion ist als f(x)=3x-9
b)
der Schnittpunkt mit der y-Achse ist f(0)=3*0-9=-9, der Punkt ist (0|-9)
der Schnittpunkt mit der x-Achse ist 0=3x-9 => x=3, der Punkt ist (3|0)
c)
hier nehmen wir den Mittelwert der beiden x-Werte der gegebenen Punkte P und Q, diese x-Werte sind 2 und 4. der Mittelwert ist 3, das setzen wir in die Funktion ein f(3)=3*3-9; f(3)=0, Die Koordinaten sind (3|0)
d)
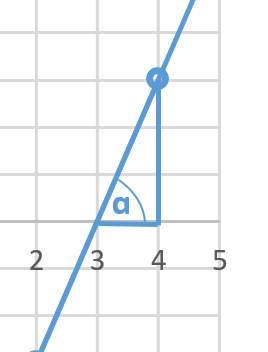
gesucht ist der Winkel ɑ, hier wenden wir den Tangens an. ɑ=\( \frac{Gegenkathete}{Ankathete} \) =\( \frac{3}{1} \) . Daraus ergibt sich der Steigungswinkel ist 71,6°. Die Schnittwinkel sind 71,6° bzw. 18,4°