Berechne die folgenden Grenzwerte (x³( 1/x² • cos(1/x²) - sin(1/x²))/x³

Question

Aufgabe:

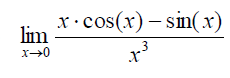
Text erkannt:

\( \lim \limits_{x \rightarrow 0} \frac{x \cdot \cos (x)-\sin (x)}{x^{3}} \)

Mein Versuch:

1. ich habe für x erstmal 0 eingesetzt und festgestellt, dass dann 0/0 herauskommt, um das zu lösen, bräucht man die "de l'Hospitalsche Regel", die haben wir noch nicht gelernt

Also habe ich versucht x³ auszuklammern

Dabei ist folgendes heraus gekommen:

x³ ( 1/x² • cos(1/x²) - sin(1/x²)
--------------------------------------
             x³ • (1)

Hier habe ich dann x³ weg gekürzt und hatte:
( 1/x² • cos(1/x²) - sin(1/x²)
--------------------------------------
                 1

Jetzt habe ich für jede Position notiert, wohin diese konvergiert
1/x² -> 0
cos(1/x²) -> 0
sin(1/x²) -> 0
1 -> 1

habe dann die 0 durch 1 geteilt und ermittelt, dass der Grenzwert = 0 ist

Kann man das so machen oder verstoße ich damit gegen irgendwelche Mathematischen Regeln, also darf man 0 / 1 teilen?

Es macht meiner Meinung nach schon Sinn, da der obere Teil immer kleiner wird und der untere Teil immer = 1 ist, also wird die Zahl immer kleiner und das ganze konvergiert gegen 0, liege ich da mit meiner Vermutung richtig?

Comments

Dabei ist folgendes heraus gekommen:

x³ ( 1/x² • cos(1/x²) - sin(1/x²)
--------------------------------------
          x³ • (1)

... das ist ganz falsch!

cos(1/x²) -> 0
sin(1/x²) -> 0

... selbst dies ist grundsätzlich falsch. Mit \(x \to 0\) läuft \(1/x^2 \to \infty\). Und die trigonemtrischen Funktionen haben im Unendlichen keinen Grenzwert!

Answer 1

Hallo,

um das zu lösen, bräucht man die "de l'Hospitalsche Regel", die haben wir noch nicht gelernt

wenn Ihr das noch nicht hattet, so kennst Du vielleicht die Reihenentwicklung von Sinus und Cosinus. Es gilt $$\cos(x)= 1-\frac{x^2}{2!} + \frac{x^4}{4!} - \dots \\ \sin(x)= x - \frac{x^3}{3!} + \frac{x^5}{5!} - \dots$$Setze dies doch oben in den Ausdruck ein$$\lim_{x\to 0}  \frac{x\cos\left(x\right)-\sin\left(x\right)}{x^{3}}$$Du wirst sehen, dass sich das ganze schlagartig vereinfacht.

Gruß Werner

Answer 2

Kontrollweg mit l´Hospital:

\(\lim \limits_{x \rightarrow 0} \frac{x \cdot \cos (x)-\sin (x)}{x^{3}} \)=\( \frac{1*cos(x)-x*sin(x)-cos(x)}{3x^2}\)=\(\lim \limits_{x \rightarrow 0}\frac{-x*sin(x)}{3x^2} \)=\(\lim \limits_{x \rightarrow 0}\frac{-sin(x)}{3x} \)=\(\frac{-cos(x)}{3} =-\frac{1}{3}\)