Prozess mit linearer Regression approximieren?

Question

Aufgabe:

Sie haben Daten die folgende Daten erheben. Ist es hier angebracht, den datengetriebenen Prozess mit einer linearen Regression zu approximieren?

Falls ja : schätzen Sie die Regressionsparameter mit Hilfe der Maximum-Likelihood-Methode aus den Daten.

Falls nein : Begründen Sie, warum eine lineare Regression nicht der richtige Ansatz ist. Geben Sie dann eine sinnvolle Alternative an und begründen Sie, warum diese in diesem Fall geeignet ist.

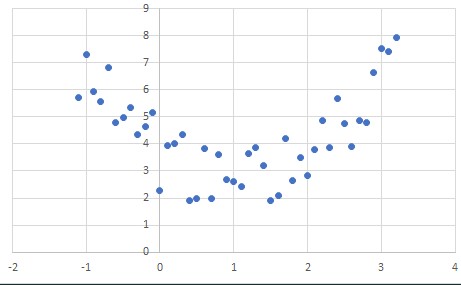
Problem/Ansatz:

Nein, da die Verteilung des erhobenen Datensatzes nicht linear verläuft. Man könnte mit der Least Square Methode schätzen, da diese unabhängig ist.


Ist das soweit korrekt oder lieg ich damit komplett falsch? Was wäre denn eine sinnvolle Alternative sonst?

Comments

Eine lineare Regression erfolgt auch mit der Least-Squares-Methode.

Was ist ein datengetriebener Prozess?

Answer 1

Aloha :)

Willkommen in der Mathelounge... \o/

Eine lineare Regression liefert eine Funktionsgleichung der Form:$$f(x)=a\cdot x+b$$Die hier vorliegenden Daten folgen jedoch offensichtlich sehr deutlich einer Parabel, also einer Funktion der Form$$g(x)=a\cdot x^2+b\cdot x+c$$Demach wäre eine Polynom-Regression nach der Gauß'schen Methode der kleinsten Fehlerquadrate vielversprechender.