Moin Leute!
Diesen Post gibt es doppelt, der alte kann gelöscht werden, da ich dort weder bearbeiten noch löschen konnte.
Ich habe leider mal wieder ein Problem mit einer Dichtefunktion und brauche bitte dringend eure Hilfe :(
Die Aufgabe ist diese:
Die folgende Dichtefunktion der Zufallsvariable \( X \) zeigt die Verteilung des Gewichts im männlichen Mittelgewicht ( \( \leq 75 k g \) ) beim olympischen Boxen.
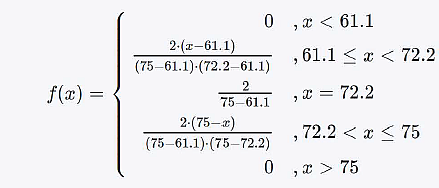
$f(x)=\left\{\begin{aligned} 0 &, x<61.1 \\ \frac{2 \cdot(x-61.1)}{(75-61.1) \cdot(72.2-61.1)} &, 61.1 \leq x<72.2 \\ \frac{2}{75-61.1} &, x=72.2 \\ \frac{2 \cdot(75-x)}{(75-61.1) \cdot(75-72.2)} &, 72.2<x \leq 75 \\ 0 &, x>75 \end{aligned}\right.$
Wie groß ist das erwartete Gewicht eines zufällig gezogenen olympischen Boxers? Beachten Sie hierbei, dass sich der Erwartungswert der Verteilung vereinfacht berechnen lässt als Mittelwert von Minimum, Maximum und Modus der Verteilung.
Erwartetes Gewicht in \( \mathrm{kg}= \) ???
Ein Olympionike möchte wissen, wie wahrscheinlich es ist, dass sein nächster Gegner zwischen einschließlich 74 und 75 kg wiegt.
Wahrscheinlichkeit für das angegebene Gewicht = ???
Um den Erwartungswert zu berechnen, liege ich richtig mit der Annahme, für jeden angegebenen Wertebereich den Mittelwert bzw. Modus zu bilden (z.B. 66,65 für 61,1 ≤ x < 72) und dann gemäß der Formel
E(X) = \( \int\limits_{-\infty}^{\infty} \) x • f(x) dx
für jeden Wertebereich den Erwartungswert auszurechnen und alles zusammen zu addieren?
Als Ergebnis hätte ich so ≈69,5772
Oder ist der Ansatz so falsch?
Für den zweiten Teil müsste laut meiner Rechnung ≈0.0257 raus kommen, richtig?
Ich danke vielmals für eure Hilfe!
Liebe Grüße,
euer Studi07