Aufgabe:
Berechnen Sie die Wahrscheinlichkeit bei einem Bingo Spiel mit 75 Kugeln in weniger als 6 Ziehungen ohne Zurücklegen ein Bingo zu erhalten.

Problem/Ansatz:
… Mein Ansatz wäre das so wie bei beim Lotto zu betrachten, also das mit der hypergeometrischen Verteilung zu berechnen. Es ist ja ohne Zurücklegen und ohne Reihenfolge, also es ist ja egal ob man jetzt 4 richtige in den ersten 4 Ziehungen hat oder 4 richtige in den letzten 4 Ziehungen hat (für 4 Möglichkeiten mit den 4 Zahlen)
Es gibt 8 Möglichkeiten für eine Kombination aus 5 Zahlen und 4 Möglichkeiten für eine Kombination aus 4 Zahlen.
Mein Rechenweg sieht so aus:

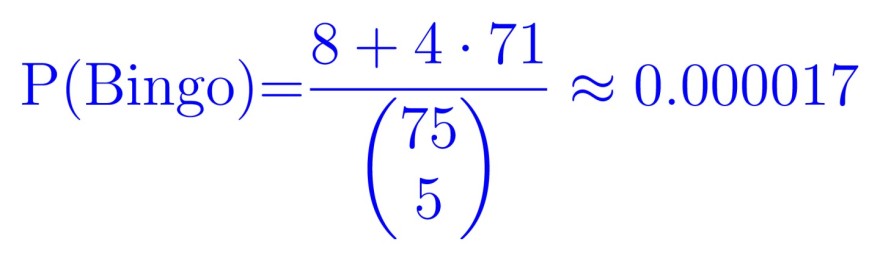
0.000017 * 100 = 0.00017% = 1 zu 58.823.53
A: Die Wahrscheinlichkeit innerhalb von 5 Ziehungen ein Bingo zu erhalten beträgt etwa 1 zu 59 Tausend.
Wäre das richtig so?