Berechnen Sie den Wert von m, für den die Wahrscheinlichkeit dafür, dass genau eine Kreuzkarte unter den …

Question

Aufgabe:

Auf einem Tisch liegen vier Kreuzkarten und m Herz- bzw. Karokarten. Sie decken nun zwei Karten auf. Berechnen Sie den Wert von m, für den die Wahrscheinlichkeit dafür, dass genau eine Kreuzkarte unter den aufgedeckten Karten ist gleich \(\frac{2}{5}\) ist.

Problem/Ansatz:

… Eine Gleichung aufstellen wo:

... = \(\frac{2}{5}\)

Doch wie bringe ich die 4 und m in die Gleichung ein?

Answer 1

Du gehst mit der normalen Pfadregel an diese Aufgabe.

\( 2 \cdot \frac{4}{4 + m} \cdot \frac{m}{3 + m} = \frac{2}{5} \) → m = 1 oder m = 12

Comments

Stimmt es kann ja auch noch m = 1 rauskommen.

Habe beim Umstellen dieser Gleichung nach m, bei der Wurzel schon abgeschaltet, da ja keine negative Zahl für die Anzahl der Karten rauskommen kann.

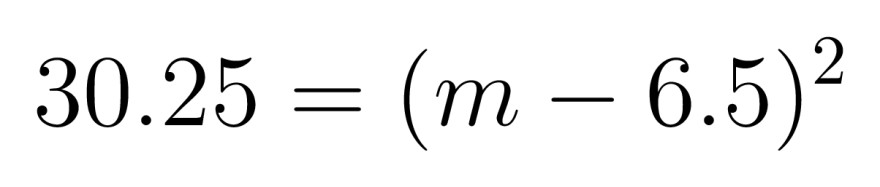
Finde es interessant, dass es einmal die Möglichkeit gibt, mit weniger als 4 Karten und einmal mit mehr als 4 Karten, auf eine Wahrscheinlichkeit von 40% zu kommen.

---

Finde es interessant, dass es einmal die Möglichkeit gibt, mit weniger als 4 Karten und einmal mit mehr als 4 Karten, auf eine Wahrscheinlichkeit von 40% zu kommen.

Beachte, dass du bei m = 1 insgesamt 5 Karten hast und bei m = 12 insgesamt 16 Karten. Man hat NIE weniger als 4 Karten.

---

Finde es interessant, dass es einmal die Möglichkeit gibt, mit weniger als 4 Herzkarten und einmal mit mehr als 4 Herzkarten, auf eine Wahrscheinlichkeit von 40% zu kommen.

---

Ich wunder mich in diesem Fall eher über die Art der Fragestellung.

"Berechnen Sie den Wert von m, ..." bedeutet eigentlich es gibt genau einen Wert für m für den das Zutrifft und den soll man berechnen.

Eigentlich sollte die Fragestellung besser lauten: "Berechnen Sie die Werte von m, ..."