Aufgabe:
Brieftauben werden bei Wettkämpfen an einen Ort gebracht, von dem sie selbstständig wieder
zurück nach Hause fliegen. Bei der vorliegenden Aufgabe wird angenommen, dass Brieftauben
stets den kürzesten Weg nach Hause suchen.
Die nachstehende Grafik zeigt einige Städte in Oberösterreich, in denen es Taubenzüchter/in-
nen gibt, in einem Koordinatensystem. Dabei entspricht eine Längeneinheit im Koordinaten-
system einer Entfernung von 10 Kilometern.
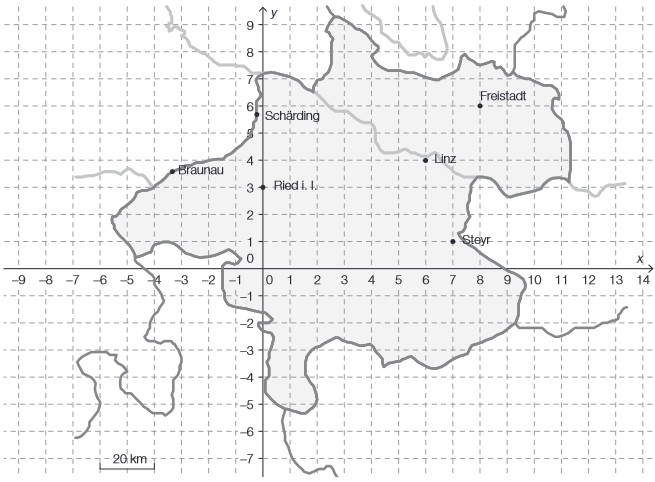
c) Eine Taube startet in Linz. Sie fliegt eine Strecke von 67,08 km Länge in Richtung des
Vektors (-1 -2)
– Ermitteln Sie die Koordinaten desjenigen Vektors, den die Taube von Linz bis zu ihrem
Ziel entlangfliegt. Geben Sie die Koordinaten dabei in den Längeneinheiten des obigen
Koordinatensystems an.
Problem/Ansatz:
Hab trotz langes Überlegen keine Ahnung wie dies zu berechnen geht. Bitte um Lösungsansatz