Berechnen Sie die Koordinaten des höchsten Punktes des Höhenprofils.

Question

Text erkannt:

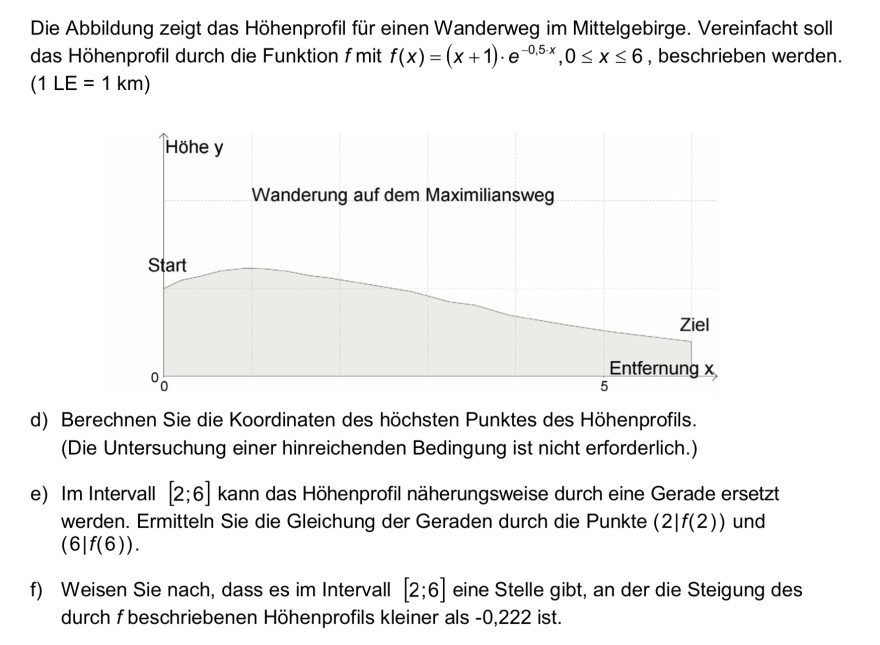
Die Abbildung zeigt das Höhenprofil für einen Wanderweg im Mittelgebirge. Vereinfacht soll das Höhenprofil durch die Funktion \( f \) mit \( f(x)=(x+1) \cdot e^{-0,5 \cdot x}, 0 \leq x \leq 6 \), beschrieben werden. (1 LE = \( 1 \mathrm{~km} \) )
Höhe y
Wanderung auf dem Maximiliansweg
Start
Ziel
Entfernung \( x \)
d) Berechnen Sie die Koordinaten des höchsten Punktes des Höhenprofils.
(Die Untersuchung einer hinreichenden Bedingung ist nicht erforderlich.)
e) Im Intervall \( [2 ; 6] \) kann das Höhenprofil näherungsweise durch eine Gerade ersetzt werden. Ermitteln Sie die Gleichung der Geraden durch die Punkte \( (2 \mid f(2)) \) und \( (6 \mid f(6)) \).
f) Weisen Sie nach, dass es im Intervall \( [2 ; 6] \) eine Stelle gibt, an der die Steigung des durch \( f \) beschriebenen Höhenprofils kleiner als \( -0,222 \) ist.

Aufgabe:

Aufgabe d habe ich schon gelöst…

Aber wie soll man bei e und f vorangehen?

Muss man die Ableitungen verwenden?

Übrigens sind die Gleichungen

f(x) = (x*1) e^-0.5x

g(x) = x+ 1

Answer 1

Hallo

e) einfach f(2) und f(6) berechnen, dann die Gerade durch die 2 Punkte .

f) f' hast du ja schon bei a) bestimmt, jetzt suchen f'<-0,222. dazu f'(x1)=-0,222, und dann f' für ein x2<6 suchen so dass f'(x2)<-0,222 ist, wenn du f ansiehst kannst du feststellen ob x2<x1 oder >x1

Gruß lul