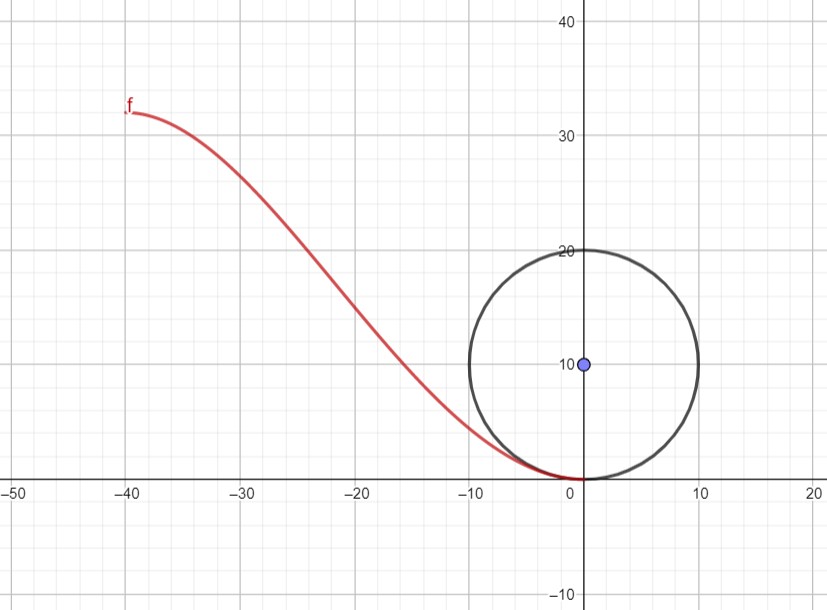
f(x) = - 1/160000·x^4 + 1/2000·x^3 + 1/20·x^2
1) Bestimmen Sie den Bereich der Abfahrt, in dem der Neigungswinkel von 45° überschritten wird.
f'(x) = -1 --> x = -29.55217741 ∨ x = -13.17592838 ∨ x = 102.7281058
Im Intervall von ca. [-29.55 ; -13.18] wird der Neigungswinkel von 45 Grad überschritten.
2) Der Krümmungskreis im Nullpunkt C ist also der für die Achterbahn gesuchte Looping. Weisen Sie nach, dass der Kreis mit dem Mittelpunkt (0/10) und dem Radius 10 der Krümmungskreis der Funktion g im Punkt 0 ist.
f'(0) = 0 → Waagerechte Tangente in C daher befindet sich der Kreismittelpunkt senkrecht über C.
Krümmung bzw. Krümmungsradius
k = f''(0)/√(1 + f'(0)^2)^3 = 0.1
r = 1/0.1 = 10
Damit beträgt der Radius 10 und der Kreismittelpunkt muss 10 Einheiten über C sein.
Skizze