Aufgabe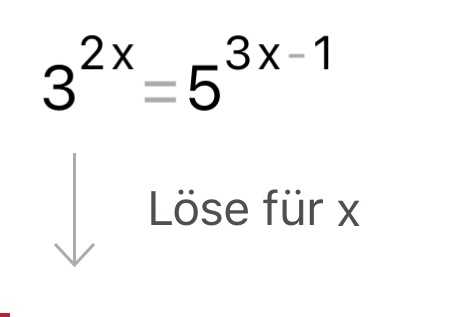
Text erkannt:
\( 3^{2 x}=5^{3 x-1} \)
Löse für \( x \)
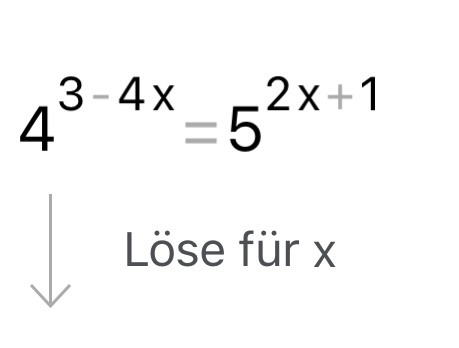
Text erkannt:
\( 4^{3-4 x}=5^{2 x+1} \)
Löse für \( \mathrm{x} \)
Problem/Ansatz:
Hallo!
Das ist hier mein erster Thread in diesem Mathe Forum, also verzeit mir bitte etwaige Fehler:)
Problem: Die beiden Aufgaben muss ich mit dem Logarithmus lösen. Gegeben ist die Lösung und als Aufgabe steht:
„Löse die Exponentialgleichung mit dem einfachsten Lösungsweg mit dem Logarithmus“
Lösung 1. Aufgabe = 0,6117
Lösung 2. Aufgabe = 0,2909
Ich hoffe wirklich auf Hilfe, da ich daran schon seit Tagen verzweifle :)
Beste Grüße
Luca