Anwendungsorientierung im Mathematikunterricht
Die aktuellen Rahmenpläne für Mathematik sind in allen Bundesländern hauptsächlich „anwendungsorientiert“ und die Textaufgaben behandeln fast nur außermathematische Zusammenhänge, deren Lösungen mit Hilfe der Mathematik gelingen sollen. Erst in zweiter Linie und eher selten geht es um innermathematische Probleme. Die ursprüngliche von Didaktikern erarbeitete Stoffauswahl und Stoffverteilung stammt jedoch nicht aus Anwendungsproblemen, sondern ist historisch und lerntheoretisch begründet. Weil das nicht ernsthaft angetastet werden kann und konnte, ist eine erhebliche Spannung zwischen den neueren Rahmenplänen und dem überlieferten Stoffplan unvermeidlich. Natürlich werden solche Widersprüche von Richtlinienkommissionen zwar erzeugt, aber nicht aufgelöst, sondern an Schulbuchschreiber und Lehrer zur methodischen Bewältigung weitergereicht. Das hat zu sehr vielen „eingekleideten Aufgaben“ geführt, welche Pseudoanwendungen und Übersimplifikationen enthalten. Welche Probleme aus dem Leben der Schüler*innen benötigen zu ihrer Lösung den größten gemeinsamen Teiler, irrationale Zahlen oder die Pi-Berechnung? Derartige Aufgaben findet der Schulbuchautor oder der Lehrer nun einmal nicht ohne Verzerrungen der historischen Ideenentwicklung oder der tatsächlichen Relevanz der jeweiligen Inhalte. Es ist für jeden mathematisch Gebildeten offensichtlich, dass die Herleitung des mathematischen Schulstoffs aus Anwendungen zwar gelegentlich gelingen kann aber, dass die Legitimation der üblichen Sekundarstufenmathematik allein aus Anwendungen eine falsche Vorstellung vom Wesen der Mathematik und ihrer gesellschaftlichen Bedeutung hervorrufen würde.
Der Mathematikunterricht an allgemeinbildenden Schulen kann den Anspruch permanenter Anwendungsorientierung prinzipiell nicht einlösen, weil er
- sinnvollerweise vom „Einfacheren“ zum „Komplizierteren“ fortschreitet,
- weitgehend die historische Entwicklung der Mathematik nachzeichnet,
- lern- und entwicklungspsychologisch vorgeht.
In manchen Rahmenplänen (z.B. Hess. KM 1995) findet man erstaunlicherweise dennoch Formulierungen, wie: „Im Mathematikunterricht sollen die Schülerinnen und Schüler erkennen, dass das mathematische Denkgebäude als wichtiges Produkt des menschlichen Geistes in sich stimmig ist.“
Das hieße doch, dass Mathematikunterricht vermitteln sollte, wie das mathematische Denkgebäude entstanden ist und sich bis heute entwickelt. Dazu gehörte dann auch das Erlebnis des individuellen Wissensgewinns. Wenn man die Forderung nach dem Erlebnis mathematischen Wissensgewinns auch noch an die Forderung der Anwendbarkeit koppelt, wird es nahezu unmöglich, sinnvolle Mathematikaufgaben zu stellen. Seine Haltung zur Anwendungsorientierung des Mathematikunterrichtes drückt Lutz Führer so aus:
Die Mathematik oberhalb der Grundschule ist nicht aus dem Wunsch entstanden, Jugendlichen ihre Umwelt zu erschließen. Sie ist in ihrer Substanz nicht „lebensnäher“ als Newtons Physik, Marxsche Wirtschaftstheorie, Goethes Faust oder Beethovens Neunte. So zu tun, als wäre das anders, grenzt an Betrug und ist zumindest intellektuell unredlich (Führer 1997).
Schüler*innen, welche die rationalen Zahlen ausgiebig kennengelernt haben, müssen eines Tages mit der Frage nach der Seitenlänge eines Quadrates mit der Fläche 2 konfrontiert werden. Dabei ist es gleichgültig, ob die Schüler*innen darin einen Bezug zu ihrem Leben erkennen. Vielmehr geht es um die mathematisch relevante Erkenntnis, dass die gesuchte Länge nicht rational sein kann.
Vorschlag einer Unterrichtsstunde mit individuell verfügbarem Einsatz eines Computer-Algebra-Systems (CAS) um dem verbreiteten Ruf nach digitalem Lernen zu folgen:
Thema:
Welche Länge hat die Diagonale eines Quadrates mit der Seitenlänge 1?
Einführende Aufgaben:
1. Welche Fläche hat ein Quadrat mit der Seitenlänge 1?
2. Welche Fläche hat ein Quadrat, das die Diagonalenlänge des Quadrates aus Aufgabe 1 als Seitenlänge hat? Tipp: Zerlege in Teilflächen.
Die Lösung von Aufgabe 2. Wird an der Tafel demonstriert:
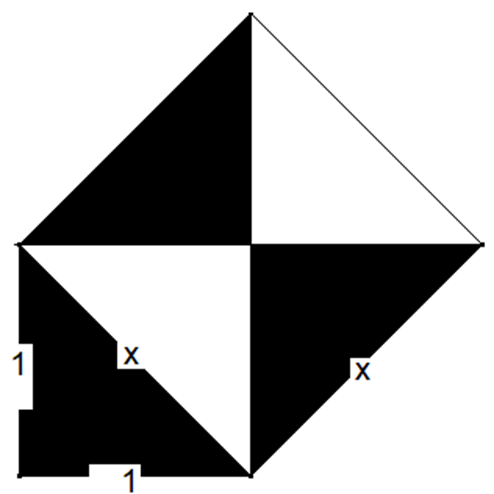
Weiterführende Aufgaben:
3. Was gilt also für x?
Die Antwort wird an der Tafel festgehalten: x2=2.
Einen Weg, um x zu finden liefert CAS im exakten Modus als √2 und im Ungefähr-gleich-Modus als 1.414213562. Es ergibt sich die Frage nach der Genauigkeit dieses Ergebnisses. Zur Beantwortung dieser Frage, wird ein wenig ausgeholt und zunächst folgende Aufgabe gestellt:
4. Ergänze die folgende Tabelle mit Hilfe von CAS
(√2-1)2
| 3 – 2√2 |
(√2-1)4
| |
(√2-1)8
|
|
(√2-1)16
|
|
und berechne dann die rechte Spalte im Ungefähr-gleich-Modus.
Die Lösung wird an der Tafel demonstriert:
(√2-1)2
| 3 - 2 √2
| 0.1715728752
|
(√2-1)4
| 17-12√2
| 0.02943725152
|
(√2-1)8
| 577 – 408√2
| 0.0008665517771
|
| (√2-1)16 | 665857 – 470832√2
| 0
|
5. Zeige, dass die Annahme 665857 – 470832√2 = 0 zu einer rationalen Lösung für √2 führt und führe die Annahme zum Widerspruch. (Tipp: Endstellenbetrachtung nach Quadrieren von √2).
Die Lösung wird an der Tafel demonstriert:
√2=\frac{...7}{...2} und dann 2=\( \frac{...9}{...4} \) . Widerspruch.
6. Sei u eine ungerade und g eine gerade Zahl. Zeige, dass es eine Darstellung (√2-1)(2^n ) = u - g√2 für alle n∈N gibt.
Beweis durch vollständige Induktion. Der Induktionsanfang steht in der Lösung von Aufgabe 4. Der Induktionsschluss erfolgt durch Verdopplung des Exponenten bzw. Quadrieren der Basis.
u und g können so gewählt werden, dass (√2-1)^((2^n ) )= u – gˑ√2. Dann ist u/g eine gute Näherung für √2, die aber nicht exakt sein kann (analog der Lösung von Aufgabe 5).
Quelle
(Lutz Führer 1997_PdMU.pdf (uni-frankfurt.de) aufgerufen am 12.10.2022)