Aufgabe:
Gegeben ist ein in ein Rechteck eingeschriebenes Dreieck. Stelle ein Term für den Flächeninhalt des Dreiecks in Abhängigkeit von x auf. Siehe Bild. Für welches x wird der Flächeninhalt des Dreiecks minimal? Die Rechtecksseiten betragen AB = 5 cm. AC=3cm
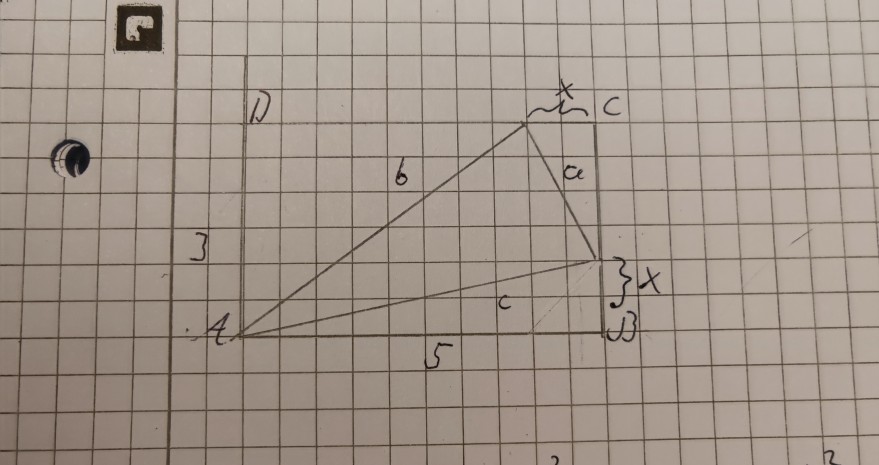
Problem/Ansatz:
Also wie man einen Verhalt auf ein minimum oder Maximum überprüft weiß ich. Nur nicht bei diesem Beispiel. Ich kann keine Flächeninhaltsformel in Abhängigkeit von x angeben. Ich kann a^2 b^2 und c^2 in Abhängigkeit von x angeben durch den Satz des Pythagoras. Ich komme aber auf keine Flächeninhaltsformel. Der Sinussatz bringt mich nicht weiter, da kein Winkel gegeben ist. Der Kosinussatz bringt mich auch nicht weiter. Und da es kein Oberstufenmaterial ist, dürfte die Lösung nicht allzu komplex sein. Vielleicht übersehe ich ja etwas.