Die (Fermat) Gleichung \( x^{3}+ y^{3}=1 \) hat bekanntlich keine rationalen Lösungen.
Ich möchte hier zeigen, wie man das eventuell einfacher herleiten kann.
+ Meine Frage: Wäre das prinzipiell eine Möglichkeit oder gibt es generelle Probleme?
Problem/Ansatz:
In der Abbildung ist die Funktion \( x^{3}+ y^{3}=1 \) (rot) dargestellt.
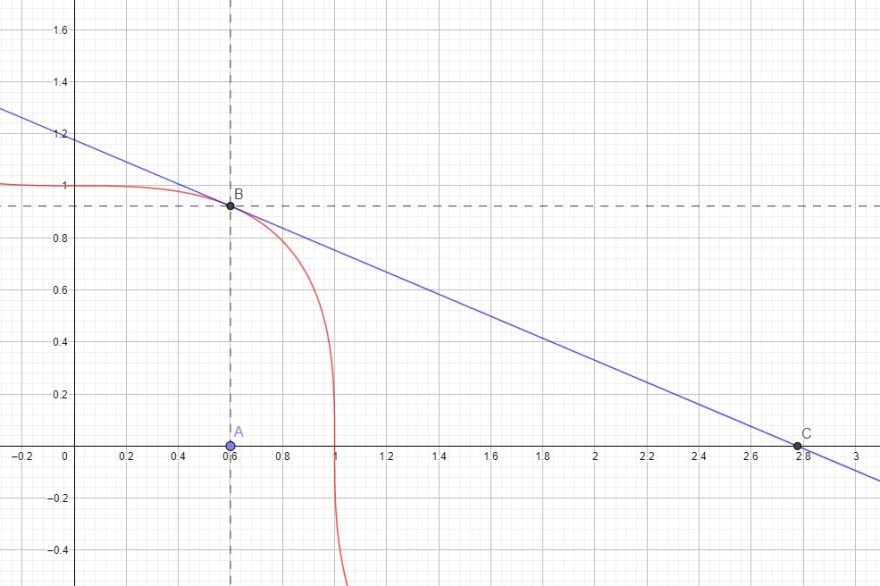
Die Funktion lässt sich auch wie folgt schreiben: \( y=\sqrt[3]{1-x^{3}} \)
Die erste Ableitung der Gleichung ist \( y'=-\dfrac{x^2}{(\sqrt[3]{1-x^{3}})^{2}} \).
Setzt man im Punkt B die Koordinaten \( x_{0} \) und \( y_{0} = \sqrt[3]{1-x_{0}^{3}} \) ein, erhält man eine Tangente (blau)
mit den Anstieg \( -\dfrac{(x_{0})^{2}}{(y_{0})^{2}} \)
Die Tangente bildet mit der x-Achse und der Senkrechten durch den Punkt B ein rechtwinkliges Dreieck ABC.
Der Betrag des Anstiegs der Tangente \( \dfrac{(x_{0})^{2}}{(y_{0})^{2}} \) ist der Tangens des Winkels zwischen der Tangente und der x-Achse, also ist gleich dem Verhältnis der Katheten AB / AC.
Es soll nun aus dem rechtwinkligen Dreieck ABC ein ähnliches Dreieck konstruiert werden, bei dem die Seitenlängen ein (primitives) Pythagoreische Tripel bilden.
Das rechtwinklige Dreieck ist mit dem Anstieg der berechneten Tangente in den Seitenverhältnissen eindeutig festgelegt.
Die Idee der Beweisführung ist nun folgende:
Es soll gezeigt werden, dass der Punkt B keine rationalen Koordinaten \( x_{0} , y_{0} \) hat.
Angenommen, die Koordinaten \( x_{0} , y_{0} \) wären rational.
Dann wäre der Betrag des Anstiegs der Tangente \( \dfrac{(x_{0})^{2}}{(y_{0})^{2}} \) ebenfalls rational.
Das gesuchte (primitive) Pythagoreische Tripel müsste dann Katheten AB und AC haben, deren Längen beide gleichzeitig Quadratzahlen sind: \( \dfrac{(x_{0})^{2}}{(y_{0})^{2}} = AB / AC \) (teilerfremd)
Da es aber kein (primitives) Pythagoreische Tripel gibt, dessen beide Kathetenlängen gleichzeitig Quadratzahlen sind, kann auch \( \dfrac{(x_{0})^{2}}{(y_{0})^{2}} \) nicht rational sein.
Damit kann aber auch \( x_{0} , y_{0} \) nicht rational sein und \( x^{3}+ y^{3}=1 \) hat keine rationalen Lösungen.