Berechne den maximal zu erreichenden Flächeninhalt von dem gleichschenkligen Dreieck in Abhängigkeit von x.

Question

Aufgabe:

Einem gleichseitigen Dreieck mit dem Flächeninhalt 9*√3  wird ein gleichschenkliges Dreieck in abgebildeter Art und Weise eingeschrieben. Berechne den maximal zu erreichenden Flächeninhalt von dem gleichschenkligen Dreieck in Abhängigkeit von x.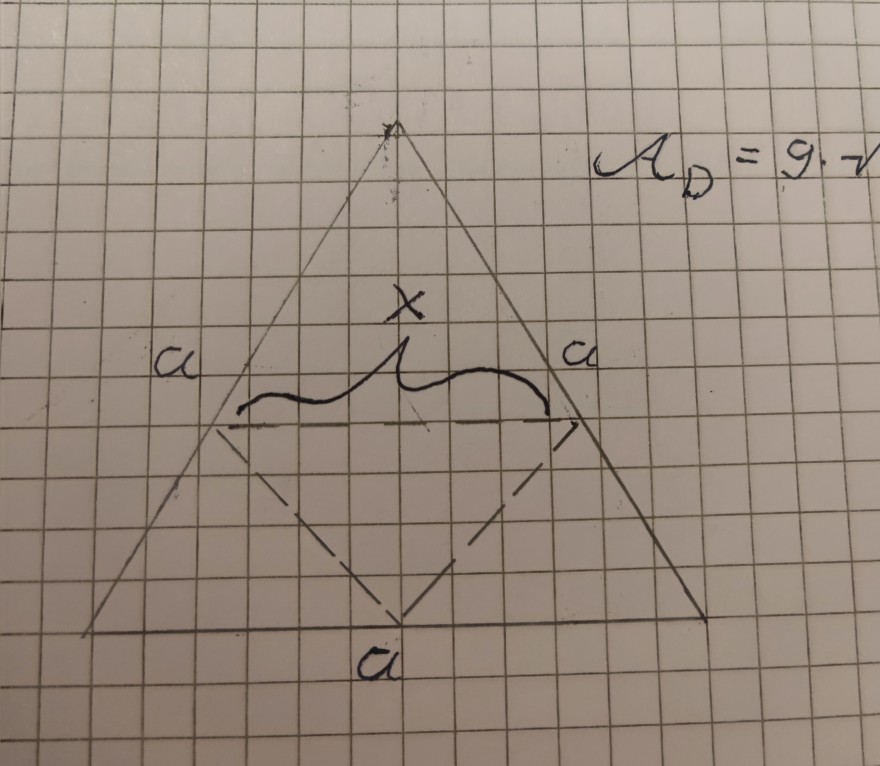

Problem/Ansatz:

Ich besitze leider keine Lösungen zu dieser Aufgabe. Es wäre sehr lieb wenn mir jemand meine Lösung validieren könnte.

Die Dreiecksseite a beträgt 6 cm.

Der maximale Flächeninhalt wird mit x=3 cm erreicht und beträgt \( \frac{9×√3}{4} \) cm^2

Answer 1

Du solltest erstmal a und h bestimmen. Dann würde ich die rechte Dreiecksseite als lineare Funktion ins Koordinatensystem einzeichnen.

Meinst du das du das hinbekommst?

Comments

Ja klar. Habe die Aufgabe ja schon fertig. a= 6 cm.

A= 9*√3

A = \( \frac{1}{4} \)\( a^{2} \) * \( \sqrt{3} \)

Umstellen: a= 6

h= \( \frac{1}{2} \) a ×\( \sqrt{3} \)

h = 3×\( \sqrt{3} \)

---

Einen Moment. Ich habe gerade eine. Kleinen Rechenfehler in meiner Rechnung entdeckt. ( Nicht die Rechnung die hier zu sehen ist. Beim Aufstellen der Funktionsgleichung)

---

Ach doch nicht. Hatte es nur anders ausgedrückt.

---

Ich hätte jetzt die Fläche des Dreiecks mit

A = 1/2 * x * f(x/2)

aufgestellt. Davon dann die Ableitung gleich Null setzen.

---

Die Ableitungen habe ich noch nicht als Thema. Auf welche Lösung würdest du denn kommen wenn du ableitest?

---

Ableitungen brauchst bdu nicht. Quadratischen Funktionen haben ihren extremen Wert im Scheitelpunkt.

---

Faktorisiert sieht die Flächenfunktion wie folgt aus

A = 3/2·√3·x - √3/4·x^2 = √3/4·x·(6 - x)

Wenn man weiß, dass die Extremstelle exakt der Mittelwert der Nullstellen ist, ergibt sich einfach

x = 3

---

Okay perfekt. Dankeschön!

Answer 2

Die Höhe des Dreiecks oben in der Spitze ist (wegen der Ähnlichkeit zum Gesamtdreieck) \( \frac{\sqrt3}{2}x \) und diie Höhe des darunter liegenden gesuchten Dreiecks demzufolge \( \frac{\sqrt3}{2}a \)-\( \frac{\sqrt3}{2}x \)=\( \frac{\sqrt3}{2}(a-x) \). Damit hast du Grundseite und Höhe deines gesuchten Dreiecks und kannst damit einen Term für seinen Flächeninhalt aufstellen (und diesen anschließend maximieren).

Comments

Diese Rechnung verstehe ich leider nicht ganz. Aber wie in meiner Frage geschrieben, habe ich die Aufgabe ja schon fertig. Trotzdem Danke für den Hilfeversuch ,)

---

Diese Rechnung verstehe ich leider nicht ganz.

Diesen Zustand würde ich (auch in deinem Interesse für mögliche zukünftige Aufgaben) gern beheben.

Was konkret verstehst du nicht?

---

Das Dreieck in Anhängigkeit von x ist kein gleichseitiges. Und damit ist die Höhe von x nicht zwangsweise mit \frac{1}{2}\( \sqrt{3} \)x zu berechnen

---

Ich habe nur eben deine Rechnung nicht ganz nachvollziehen können. Ich habe die Aufgabe schon fertig, bin aber anders rangegangen. Ich verstehe jetzt was du meinst mit deiner Herangehensweise aber das Dreieck unten ist wie gesagt kein gleichseitiges ( nicht zwangsweise, außer bei einem speziellen Fall).

---

Meine ursprüngliche Frage war ob mein Ergebnis richtig ist: bei x=3 cm wird A maximal mit A= \( \frac{9×√3}{4} \)

---

Ich sprach zunächst von den Dreieck OBEN IN DER SPITZE!

Es ist gleichseitig mit der Seitenlänge x und hat die Höhe

 \( \frac{\sqrt3}{2}x \)

---

Nein nein. Das ist nur die Skizze. Ich hätte die Seite x auch genau so gut wo anders einzeichnen können.

---

Ich bin das Problem so angegangen:

\( \frac{a}{h} \) = \( \frac{x}{h-h(x)} \)

Umstellen

Höhe auf x = h - x/\( \frac{a}{h} \)

Funktion = \( \frac{1}{2} \) × x ×( h - x/\( \frac{a}{h} \))

---

Nein nein. Das ist nur die Skizze. Ich hätte die Seite x auch genau so gut wo anders einzeichnen können.

Das ändert nichts dran, dass auch mit diesesm neuen Wert x für die Seitenlänge eines gleichseitigen Dreiecks die Höhe dieses neuen Dreiecks  \( \frac{\sqrt3}{2}x \)  gewesen wäre.

---

Wieso das denn? Sagen wir mal x ist ungleich a im oberen Dreieck. Dann gilt doch nicht mehr für die höhe des oberen Dreiecks \( \sqrt{3} \) * \( \frac{1}{2} \)*x. Weil das ja die Formel für die Höhe eines gleichseitigen Dreiecks ist, welche die Spitze dann nicht mehr wäre.

---

Hallo,

das von abakus gelb markierte Dreieck ist gleichseitig. x verläuft parallel zur unteren Seite a und die Winkel betragen alle 60°.

---

Achso. Jetzt verstehe ich was er meint. Stimmt, kann man ja auch als zentrische Streckung betrachten oder mittels Strahlensatz. Vielen Dank!