Aufgabe:
Die Konstrukteure einer kleinen Firma haben einen neuartigen Flugzeugflügel entworfen. Dabei werden die Graphen der Funktionen f und h zwischen ihren Schnittpunkten S, und S₂ zur Modellierung des Querschnitts dieses Flugzeugflügels verwendet. Es gilt: 1 LE = 1 dm.
1. An einer Stelle hat der Flugzeugflügel eine maximale vertikale Höhe. Diese Stelle kann mithilfe der Differenzfunktion d mit d(x) = f(x)-h(x) bestimmt werden. Die maximale vertikale Höhe darf 7,15 dm nicht überschreiten. Untersuchen Sie, ob die Konstrukteure dies beachtet haben.
2. Bestimmen Sie die Querschnittsfläche des Flugzeugflügels mithilfe der Differenzfunktion d.
Ohne Nachweis dürfen Sie verwenden, dass D mit D(x)=(x²-15/2^x-75) ⋅ e^-0.1x
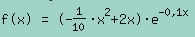
Text erkannt:
\( f(x)=\left(-\frac{1}{10} \cdot x^{2}+2 x\right) \cdot e^{-0,1 x} \)
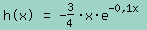
Text erkannt:
\( h(x)=-\frac{3}{4} \cdot x \cdot e^{-0.1 x} \)
Wie löse ich diese Aufgaben?