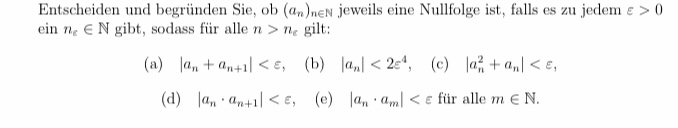
Text erkannt:
Entscheiden und begründen Sie, ob \( \left(a_{n}\right)_{n \in \mathbb{N}} \) jeweils eine Nullfolge ist, falls es zu jedem \( \varepsilon>0 \) ein \( n_{e} \in \mathbb{N} \) gibt, sodass für alle \( n>n_{e} \) gilt:
(a) \( \left|a_{n}+a_{n+1}\right|<\varepsilon \),
(b) \( \left|a_{n}\right|<2 \varepsilon^{4} \),
(c) \( \left|a_{n}^{2}+a_{n}\right|<\varepsilon \),
(d) \( \left|a_{n} \cdot a_{n+1}\right|<\varepsilon \),
(e) \( \left|a_{n} \cdot a_{m}\right|<\varepsilon \) für alle \( m \in \mathbb{N} \).
Aufgabe:
Ich habe Probleme bei dieser Aufgabe. Kann mir jemand helfen?
A habe ich schon gezeigt, dass es nicht stimmt