Aufgabe:
Text erkannt:
Hausaufgabe 2.5 [5 Punkte]
Es sei \( n \geq 4 \) und wir stellen uns vor, eine Springerfigur stehe auf dem linken unteren Feld eines ansonsten leeren \( (n \times n) \)-Schachfeldes. Zeigen Sie, dass die Figur in \( 2 \cdot\left\lfloor\frac{n+1}{3}\right\rfloor \) Zügen das obere rechte Feld erreicht. Dabei bezeichnet \( \lfloor q\rfloor \in \mathbb{Z} \) für \( q \in \mathbb{Q} \) die größte ganze Zahl, die höchstens so groß ist wie \( q \). (Auch hier dürfen Sie aus der Schule bekannte Regeln für das Rechnen mit Zahlen aus \( \mathbb{Q} \) verwenden.)
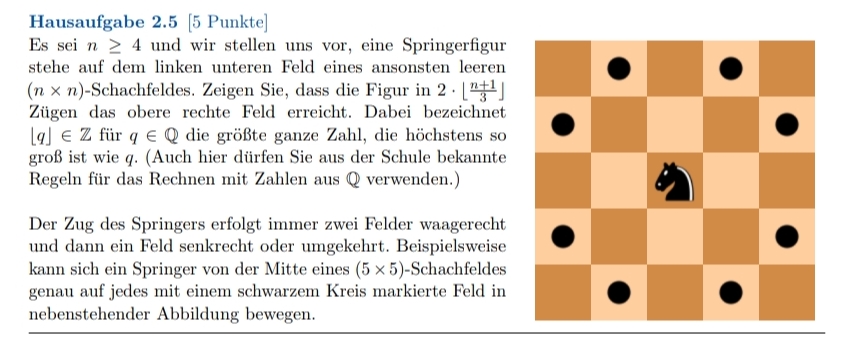
Der Zug des Springers erfolgt immer zwei Felder waagerecht und dann ein Feld senkrecht oder umgekehrt. Beispielsweise kann sich ein Springer von der Mitte eines \( (5 \times 5) \)-Schachfeldes genau auf jedes mit einem schwarzem Kreis markierte Feld in nebenstehender Abbildung bewegen.
Problem/Ansatz:
Mein Ansatz für die Aufgabe ist eine Induktion für eine Ungleichung.
Wegen n x n, würde ich eine Induktion von n^2 > als der Ausdruck 2*q.
Bin ich damit auf der richtigen Spur, oder gibt es einen besseren Ansatz.