Extremwertaufgabe: Abstand zwischen zwei Punkten

Question

Aufgabe:

Ich soll den kürzesten Abstand zwischen Punkt Q eines Graphen mit der Funktion f(x)=0.5x² und dem Punkt P(6/0) berechnen.

Problem/Ansatz:

Mir ist zwar bewusst, dass es eine Extremwertaufgabe ist, aber ich komme einfach nicht auf die richtige Lösung.

Ich hoffe, Jemand kann den Lösungsweg erklären. Die Lösung sollte Q(2/2) sein.

Danke im Voraus.

Comments

Ich soll den kürzesten Abstand ... berechnen. Die Lösung sollte Q(2/2) sein.

Q ist nicht die Lösung. Q ist der Punkt auf dem Graphen im kürzesten Abstand zu P.

Der Abstand beträgt \( \sqrt{20} \)

---

Ich habe zuerst schon versucht, den Abstand zu berechnen, aber die Lösung ist laut meinen Unterlagen Q(2/2). Die Aufgabe selbst ist wohl zu wenig genau formuliert. Ich entschuldige mich dafür.

---

Ist ja nicht Dein Problem, wenn die Fachkraft eine Musterlösung abgibt, die nicht das beantwortet was sie als Aufgabe gefragt hat.

Answer 1

Aloha :)

Die Entfernung zwischen den Punkten \((6|0)\) und \((x|f(x))=(x|\frac12x^2)\) beträgt:$$d(x)=\left\|\binom{x}{\frac12x^2}-\binom{6}{0}\right\|=\left\|\binom{x-6}{\frac12x^2}\right|=\sqrt{(x-6)^2+\left(\frac12x^2\right)^2}$$Anstatt den Abstand \(d(x)\) zu minimieren, können wir genauso gut das Quadrat minimieren, brauchen uns dafür aber nicht mit der Wurzelfunktion zu beschäftigen:$$d^2(x)=(x-6)^2+\left(\frac12x^2\right)^2=x^2-12x+36+\frac14x^4$$

Die Extremwerte dieser Funktion finden wir dort, wo die Ableitung zu Null wird:$$0\stackrel!=(d^2(x))'=\pink{2x}-12+x^3=x^3\blue{+2x^2}\pink{+6x}\blue{-2x^2}\pink{-4x}-12$$$$\phantom0=(x^3\blue{+2x^2}\pink{+6x})-(\blue{2x^2}\pink{+4x}+12)=x(x^2+2x+6)-2(x^2+2x+6)$$$$\phantom0=(x-2)(x^2+2x+6)=(x-2)\left((x+1)^2+5\right)$$Die Summe in der zweiten Klammer ist stets \(\ge5\), daher ist die einzige Nullstelle der ersten Ableitung bei \(x=2\).

Der gesuchte Punkt auf der Parabel ist daher: \(\quad P(2|2)\).

Answer 2

vgl:

https://www.mathelounge.de/1128/minimalen-abstand-eines-punktes-einer-funktion-berechnen

Answer 3

Klicke mal hier drauf.

Answer 4

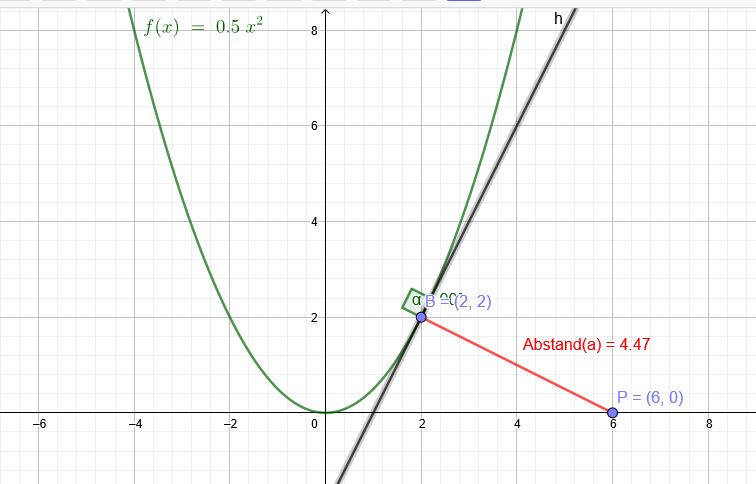
"Ich soll den kürzesten Abstand zwischen Punkt Q eines Graphen mit der Funktion f(x)=0,5x^2 und dem Punkt P(6|0) berechnen."

\(f(x)=0,5x^2    → f´(x)=x \)

Geradengleichung mit der Punkt-Steigungsform: \( \frac{y-y₁}{x-x₁}=m \)     

\( \frac{y-0}{x-6}=-\frac{1}{x} \)        \( y=-\frac{1}{x}*(x-6)=-1+\frac{6}{x} \) geschnitten mit \( y=0,5x^2  \)

\( 0,5x^2=-1+\frac{6}{x} |*x \) 

\( 0,5x^3+x=6 \)    \( x^3+2x-12=0 →x=2→y=2\)

Berechnung des Abstands zwischen \( B(2|2)    und P(6|0)\):   \(a=\sqrt{2^2+(6-2)^2} =\sqrt{20}=2*\sqrt{5}  \)