Wie muss a sein, damit die gleichen genau eine Lösung besitzt?

Question

ax²+ (1+a)x + 1 = 0

Wie muss a sein, damit die Gleichung genau eine Lösung besitzt?

Comments

damit die gleichen

damit die Gleichung?

Answer 1

So, dass die Diskriminante gleich null ist.

Comments

Meinst du wenn man das in die pq formel einsetzt

---

Nein, ich meine das was als 5. Gleichung in der Antwort von ggT22 steht.

Siehe auch https://de.wikipedia.org/wiki/Diskriminante#Quadratisches_Polynom

Answer 2

Forme um zu x²+(1+a)/a+1/a=0 und wende darauf die p-q-Formel an. Damit genau eine Lösung entsteht, muss der Term unter der Wurzel ((1+a)/(2a))²-1/a=0 sein. Das ist für a=1 der Fall.

Comments

Könntest du das als richtiges bruch schreiben. Zu viele schragstriche verwieren mich

---

Drehe den Kopf ca. 60 Grad un die horizontale Achse (jene, die durch die Nasenspitze geht) nach links, dann werden die Schrägstriche zu Bruchstrichen.

---

Wie steht's mit a = 0 ?

Answer 3

abc-Formel:

b^2 -4ac = 0

b= 1+a

a= a

c= 1

(1+a)^2-4*a*1 = 0

1+2a+a^2-4a =0

a^2-2a+1 =0

(a-1)^2 =0

a = 1

Comments

Gibt's eine weitere Lösung?

---

Welche sollte das sein?

---

Wie bist du auf a=1 gekommen?

ist die 1 vom Himmel gefallen?

---

Wie bist du auf a=1 gekommen?

ist die 1 vom Himmel gefallen?

Ich sehe in der ganzen Antwort von ggT22 nichts anderes als die Herleitung, warum a = 1.

Answer 4

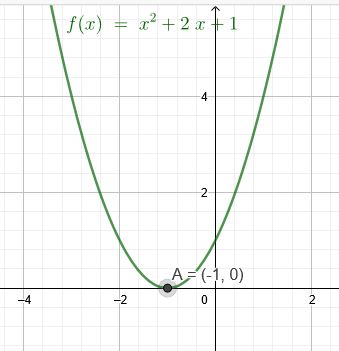
\(a*x^2+ (1+a)*x + 1 = 0 \)  mit \(a  ≠ 0\)

\(x^2+ \frac{1+a}{a}*x  =-\frac{1}{a} \)

\((x+ \frac{1+a}{2a})^2 =-\frac{1}{a}+(\frac{1+a}{2a})^2=-\frac{1}{a}+\frac{1+2a+a^2}{4a^2}=\frac{-4a+1+2a+a^2}{4a^2}=\frac{a^2-2a+1}{4a^2}=\frac{(a-1)^2}{4a^2}|\sqrt{~~} \)

\(x+ \frac{1+a}{2a} =\frac{a-1}{2a}\)

Damit es nur eine Lösung gibt muss \(\frac{a-1}{2a}=0\)   sein.  \(a=1\)

Comments

Wo steht denn, dass a ≠ 0 ist?

---

Wie bist du auf a=1 gekommen?

ist die 1 vom Himmel gefallen?