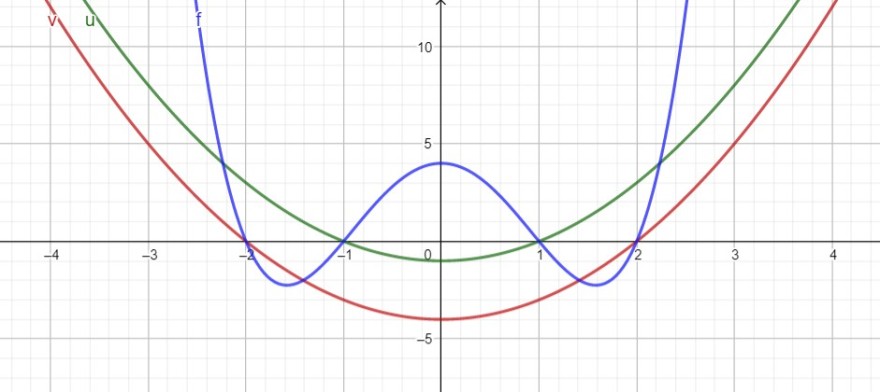
Begründen Sie die Aussage oder widerlegen Sie diese mit einem Gegenbeispiel .

Question

Aufgabe:

Begründen Sie die Aussage oder widerlegen Sie diese mit einem Gegenbeispiel . Gegeben sind die Funktionen u, v und f=u v.

a) Die Funktion f kann nicht mehr Nullstellen haben als u.

b)Die Funktion f kann nicht mehr Nullstellen haben als v.

c) Hat die Funktion u keine Nullstellen, so hat auch f keine Nullstellen.

Ein Gegenbeispiel kann auch durch einen Graphen gegeben werden.

Problem/Ansatz:

Kein Plan, bitte um Hilfe

Comments

Vom Duplikat:

Titel: Aufgabe zu Verkettung von Funktionen

Stichworte: verkettung

Ist die Aussage Richtig? Begründe oder widerlege diese mit einem Gegenbeispiel ( kann auch eine Zeichnung von einem Graphen sein)

Gegeben:

Funktionen u, v und f=u ° v. (Verkettung) 

1.Hat die Funktion u keine Nullstellen, so hat auch f keine Nullstellen.

2. Die Funktion f kann nicht mehr Nullstellen haben als v.

3. Die Funktion f kann nicht mehr Nullstellen haben als u.

Hilfe

Answer 1

Begründen Sie die Aussage oder widerlegen Sie diese mit einem Gegenbeispiel . Gegeben sind die Funktionen u, v und f = u v.

Es gilt der Satz vom Nullprodukt. f wird also Null, wenn u oder v einzeln Null werden.

a) Die Funktion f kann nicht mehr Nullstellen haben als u.

Falsch, weil die Nullstellen von v evtl. dazukommen.

b) Die Funktion f kann nicht mehr Nullstellen haben als v.

Falsch, weil die Nullstellen von u evtl. dazukommen.

c) Hat die Funktion u keine Nullstellen, so hat auch f keine Nullstellen.

Falsch. Dann sind nur die Nullstellen von v Nullstellen von f.

Skizze

Comments

Ein Vergleich der Aufgaben a) und b) lässt vermuten, dass du nicht die dem Fragesteller gestellte Aufgabe beantwortet hast.

---

Du meinst, der Fragesteller hat die ihm gestellte Frage nicht richtig wiedergegeben?

---

Nach a) macht doch b) bei einer kommutativen Verknüpfung von u und v gar keinen Sinn mehr.

---

Der Fragesteller will einfach nur auf "Nummer Sicher" gehen. Was heißt schon  kommutativ?