Auf Basis der Querschnittsfläche das Volumen eines Körpers berechnen

Question

Aufgabe:

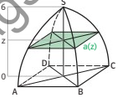
Für den abgebildeten Körper ist die Querschnittsfläche in jeder Höhe z ∈ [0;6] ein Quadrat mit der Seitenlänge a(z) = 6 - 1/6z².

Berechne das Volumen des Körpers!

Text erkannt:

\( z \)

Problem/Ansatz:

Wir haben gerade mit dem Thema begonnen, wieder mal keine Erklärungen erhalten, bitte - wenn möglich - um eine Schritt für Schritt-Anleitung - danke!

Answer 1

Schau mal dort nach der Erklärung.

https://www.mathelounge.de/93355/volumen-korper-querschnittsflache-gleichseitiges-dreieck

Hier wäre das dann wohl:

\(   \int \limits_0^6 (6- \frac{1}{6}z^2) dz \) = [ \( 6z - \frac{1}{18}  z^3 \) ]₀⁶  = 24

Answer 2

Stelle Dir aufeinandergestapelte Quadrate mit der angegebenen variablen Seitenlänge und dem daraus resultierenden Flächeninhalt vor.

\(\displaystyle \int \limits_{0}^{6}\left(6-\frac{1}{6}z^{2}\right)^{2} d z = 115,2 \)