Querschnittsfläche regelmäßiges Sechseck - Berechnung Volumen

Question

Aufgabe

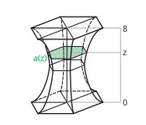
Für den abgebildeten Körper ist die Querschnittsfläche in jeder Höhe z ∈ [0;8] ein regelmäßiges Sechseck mit der Seitenlänge a(z) = 1/8 (z-4)² + 2

Berechne das Volumen des Körpers!

Problem/Ansatz:

Bitte - wenn möglich - auch hier eine Schritt für Schritt Anleitung - Danke!

Answer 1

Für den abgebildeten Körper ist die Querschnittsfläche in jeder Höhe z ∈ [0;8] ein regelmäßiges Sechseck mit der Seitenlänge a(z) = 1/8 (z-4)^2 + 2

Volumen = Integral a dz zwischen 0 0nd 8
Stammfunktion
S ( z ) = 1/8 * ( z-4)^3 / 3 + 2 * z
S ( z ) = z^3 / 24 - z^2 / 2 + 4 * z
[S] zwischen 0 und 8
V = 8^3 / 24 - 8^2 / 2 + 4 * 8  - ( 0^3 / 24 - 0^2 / 2 + 0 * 8)
V = 64 / 3

Comments

Danke, im Lösungsheft steht als Volumen 155,2.

---

Hallo blue,
ich kann bei mir keinen Fehler entedecken.
Da müssen wir einmal eine 2.Rechnung
abwarten
mfg Georg
Ich habe gerade den Fehler erkannt.
Angegeben ist nicht die Querschnittsfläche
sondern die Seitenlänge a
Ich korrigiere das nachher.

---

Lieben Dank!

---

Internet " Fläche sechseck " suchen

Seitenlänge
a ( z ) = 1/8 (z-4)^2 + 2
Fläche
A ( z ) = 3/2 * √ 3 * ( a ( z ))^2
A ( z ) = 3/2 * √ 3 * (1/8 (z-4)^2 + 2))^2

Bei Bedarf nachfragen

---

Vielen Dank!

---

Gern geschehen.

Answer 2

Stelle Dir aufeinandergestapelte Sechsecke mit der angegebenen variablen Seitenlänge und dem daraus resultierenden Flächeninhalt vor.


\(\displaystyle \int \limits_{0}^{8}\left(\frac{3\sqrt{3}}{2}(1/8 (z-4)^{2} + 2)^{2}\right) d z=\frac{448 \sqrt{3}}{5} \approx 155,19 \)