Elemantar berechenbare Reihen

Question

Aufgabe:

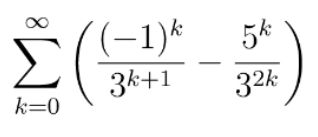
Text erkannt:

\( \sum \limits_{k=0}^{\infty}\left(\frac{(-1)^{k}}{3^{k+1}}-\frac{5^{k}}{3^{2 k}}\right) \)

Laut Augabe, soll diese Summe elementar berechenbar sein. Laut meinem Taschenrechner kommt -2 raus.

Problem/Ansatz:

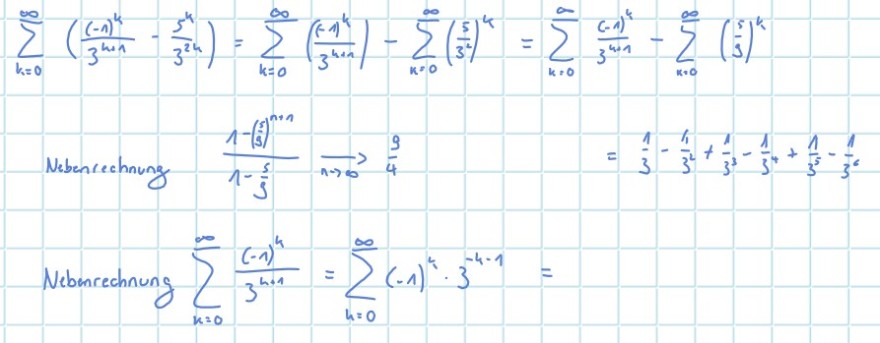
Text erkannt:

\( \sum \limits_{k=0}^{\infty}\left(\frac{(-1)^{k}}{3^{n+1}}-\frac{5^{k}}{3^{2 k}}\right)=\sum \limits_{k=0}^{\infty}\left(\frac{(-1)^{k}}{3^{k+1}}\right)-\sum \limits_{k=0}^{\infty}\left(\frac{5}{3^{k}}\right)^{k}=\sum \limits_{k=0}^{\infty} \frac{(-1)^{k}}{3^{k+1}}-\sum \limits_{k=0}^{\infty}\left(\frac{5}{3}\right)^{k} \)
Nebenrechnung \( \frac{1-\left(\frac{s}{5}\right)^{n+1}}{1-\frac{5}{3}} \underset{n \rightarrow \infty}{\longrightarrow} \frac{9}{4} \)
\( =\frac{1}{3}-\frac{1}{3^{2}}+\frac{1}{3^{3}}-\frac{1}{3^{4}}+\frac{1}{3^{5}}-\frac{1}{3^{6}} \)
Nebenrechnung \( \sum \limits_{k=0}^{\infty} \frac{(-1)^{4}}{3^{h+1}}=\sum \limits_{k=0}^{\infty}(-1)^{4} \cdot 3^{-4-1}= \)

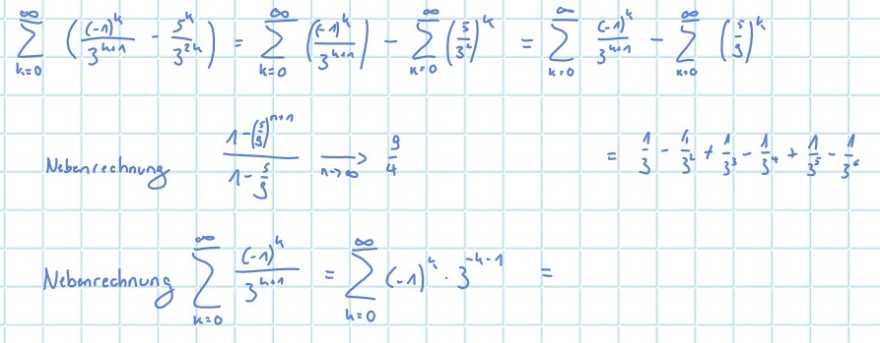
Text erkannt:

\( \sum \limits_{k=0}^{\infty}\left(\frac{(-1)^{k}}{3^{n+1}}-\frac{5^{k}}{3^{2 k}}\right)=\sum \limits_{k=0}^{\infty}\left(\frac{(-1)^{k}}{3^{k+1}}\right)-\sum \limits_{k=0}^{\infty}\left(\frac{5}{3^{k}}\right)^{k}=\sum \limits_{k=0}^{\infty} \frac{(-1)^{k}}{3^{k+1}}-\sum \limits_{k=0}^{\infty}\left(\frac{5}{3}\right)^{k} \)
Nebenrechnung \( \frac{1-\left(\frac{s}{5}\right)^{n+1}}{1-\frac{5}{3}} \underset{n \rightarrow \infty}{\longrightarrow} \frac{9}{4} \)
\( =\frac{1}{3}-\frac{1}{3^{2}}+\frac{1}{3^{3}}-\frac{1}{3^{4}}+\frac{1}{3^{5}}-\frac{1}{3^{6}} \)
Nebenrechnung \( \sum \limits_{k=0}^{\infty} \frac{(-1)^{4}}{3^{h+1}}=\sum \limits_{k=0}^{\infty}(-1)^{4} \cdot 3^{-4-1}= \)

Dies ist mein Ansatz, ich weiß durch meinen Taschenrechner, dass bei der unteren Summe 0.25 rauskommen muss, ich verstehe aber nicht wieso.

Hat da vielleicht jemand eine Idee?

Answer 1

Aloha :)

Beide Reihen für sich sind geometrische Reihen und konvergieren:$$\sum\limits_{k=0}^\infty\frac{(-1)^k}{3^{k+1}}=\sum\limits_{k=0}^\infty\frac{(-1)^k}{3\cdot 3^k}=\frac13\sum\limits_{k=0}^\infty\left(-\frac13\right)^k=\frac13\cdot\frac{1}{1-\left(-\frac13\right)}=\frac13\cdot\frac{1}{\frac43}=\frac14$$$$\sum\limits_{k=0}^\infty\frac{5^k}{3^{2k}}=\sum\limits_{k=0}^\infty\frac{5^k}{(3^2)^k}=\sum\limits_{k=0}^\infty\frac{5^k}{9^k}=\sum\limits_{k=0}^\infty\left(\frac59\right)^k=\frac{1}{1-\frac59}=\frac{1}{\frac49}=\frac94$$

Daher konvergiert auch die Differenz der Reihen:$$\sum\limits_{k=0}^\infty\left(\frac{(-1)^k}{3^{k+1}}-\frac{5^k}{3^{2k}}\right)=\frac14-\frac94=-2$$

Comments

Vielen, vielen Dank. So macht das ganze gleich mehr Sinn.

Answer 2

$$\sum \limits_{k=0}^{\infty} \left( \frac{(-1)^k}{3^{k+1}} - \frac{5^k}{3^{2k}} \right) \newline = \sum \limits_{k=0}^{\infty} \left( \frac{1}{3} \cdot \frac{(-1)^k}{3^{k}} - \frac{5^k}{9^{k}} \right) \newline = \sum \limits_{k=0}^{\infty} \left( \frac{1}{3} \cdot \left( -\frac{1}{3} \right)^k - \left( \frac{5}{9} \right)^k \right) \newline = \sum \limits_{k=0}^{\infty} \left( \frac{1}{3} \cdot \left( -\frac{1}{3} \right)^k \right) - \sum \limits_{k=0}^{\infty} \left( \left( \frac{5}{9} \right)^k \right) \newline = \frac{1}{3} \cdot \sum \limits_{k=0}^{\infty} \left( \left( -\frac{1}{3} \right)^k \right) - \sum \limits_{k=0}^{\infty} \left( \left( \frac{5}{9} \right)^k \right) \newline = \frac{1}{3} \cdot \frac{1}{1 + \frac{1}{3}} - \frac{1}{1 - \frac{5}{9}} \newline = \frac{1}{4} - \frac{9}{4} \newline = - \frac{8}{4} \newline = -2$$