lineare Gleichungen siebte Klasse

Question

Aufgabe:

Ida, Helene und Claudia untersuchen das dargestellte Muster auf eine Gesetzmäßigkeit. Sie stellen danach unterschiedliche Terme zur Berechnung der Punkteanzahl einer beliebigen Teilfigur auf.

a) Prüfe, ob ihre Terme zum Muster passen.

b) Interpretiere ihre Terme.

Problem/Ansatz:

Kann mir jemand bei dieser Aufgabe helfen

Answer 1

Wenn du von einer Ecke zur nächsten gehst, aber den letzten

Punkt in dieser Reihe   (also den auf der nächsten Ecke)

weglässt, dann hast du bei einem solchen Gang n-1

Punkte besucht. Für eine Umrundung musst du das 4 mal machen,

also sind es 4*(n-1) Punkte, wenn auf jeder Seite n Punkte liegen.

Die anderen beiden Terme besagen das gleiche, sind bloß etwas

ungeformt.

Comments

und was ist bei dem ersten term

---

2n + 2(n-2)

= 2n + 2n - 4

= 4n-4

= 4(n-1)  Passt doch !

Answer 2

Hallo,
der erste Term resultiert aus folgender Überlegung:

$${\color{blue}2n}+{\color{red}2(n-2)}$$

und weiter: das Quadrat hat 4 Seiten a \(n\) Punkte und die an den Ecken doppelt gezählten Punkte werden abgezogen

$$4n-4$$

Oder man kann das Quadrat aus vier gleich langen \((n-1)\)-Punkte-Strecken zusammen setzen.

$$4(n-1)$$

Gruß Werner

Answer 3

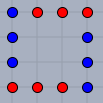
Man kann erkennen, dass die drei Formeln gleich sind.

\( \underbrace{2n+2(n-2)}_{Ida} = \underbrace{4n-4\phantom{(}}_{Claudia} = \underbrace{4(n-1)}_{Helene}\)

a)

Setze n = 3, 4 und 5 ein und vergleiche das Ergebnis mit den gezählten Punkten. Die Formeln passen.

b)

Bei der Formel I wird mit 2n die obere und die untere Punktereihe gezählt, und n-2 mal die mittleren Punktereihen, die nur aus den beiden Punkten am Rand bestehen. Minus 2, weil die Punkte in der obersten und der untersten Reihe schon mit dem ersten Summanden gezählt worden sind.

Bei der Formel C werden viermal die Punkte an den vier Rändern gezählt, abzüglich der vier Eckpunkte, damit die nicht doppelt gezählt werden.

Bei der Formel H werden viermal die Punkte an den vier Rändern gezählt, nach dieser Methode wie von Werner andernorts auf dieser Seite abgebildet: