Funktionen Aufgaben Graphen

Question

Berechne von der Funtktion -x+1 1/3 beide Schnittpunkte mit den Koordinaten Achsen

Answer 1

Hi,

Du meinst f(x) = (-x+1)^{1/3} ?

 

Für x-Achsenschnittpunkt:

f(x) = (-x+1)^{1/3} = 0

--> x = 1

S_x(1|0)

 

Für y-Achsenschnittpunkt

f(0) = (-0+1)^{1/3} = 1

S_y(0|1)

 

Grüße

Answer 2

 

f(x) = -x + 1 1/3 =

f(x) = -x + 4/3

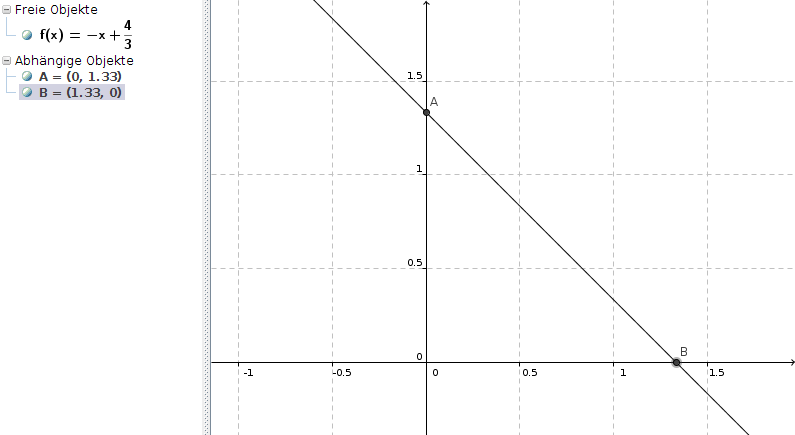
Meinst Du diese Funktion ??

 

Um den Schnittpunkt mit der y-Achse, also den y-Achsenabschnitt zu finden, setzen wir x = 0:

f(0) = 4/3

Schnittpunkt mit y-Achse S(0|4/3)

 

Und um den Schnittpunkt mit der x-Achse, also die Nullstelle zu finden, setzen wir y = 0:

f(x) = -x + 4/3 = 0

x = 4/3

Schnittpunkt mit x-Achse S(4/3|0)

 

 

Besten Gruß

Comments

Ja ich meinte diese Funktion.

Ich war verwirrt im Lösungsbuch stand Schnittpunkt mit y-Achse ist -4/3 ?

---

Mh, da hat sich wohl im Lösungsbuch ein kleiner Vorzeichenfehler eingeschlichen :-)

Die Grafik, die ich mit GeoGebra erstellt habe, zeigt ja die gleiche Lösung wie die von mir berechnete.

Oder meintest Du vielleicht statt

f(x) = -x + 4/3

f(x) = -(x + 4/3)

??

Dann wäre die Lösung -4/3 für die Schnittstelle mit der y-Achse natürlich richtig.

---

@Mathe Ass: Gewöhn dir an für Funktionsgleichungen vollständige Gleichungen anzugeben, sonst vergibst du unnötig Teilpunkte bei Tests und man versteht dich hier nicht richtig.

Entweder y = -x + 4/3 oder f(x) = -x + 4/3.

und  ausserdem statt:

"Schnittpunkt mit y-Achse ist -4/3 "

Schnittpunkt S mit y-Achse ist S(0|-4/3)         
Ein Punkt hat immer eine x- und eine y-Koordinate.

Alternative: Der y-Achsenabschnitt ist - 4/3.

Auch wenn es falsch ist, sollte es zumindest vollständig sein.

---

Nein ich meine schon die Funktion von oben.

Also naja Bücher machen Fehler.

Und diese Lösungsbuch anscheinend immer 1 pro Seite.

Zumindestens bei vielen Seiten