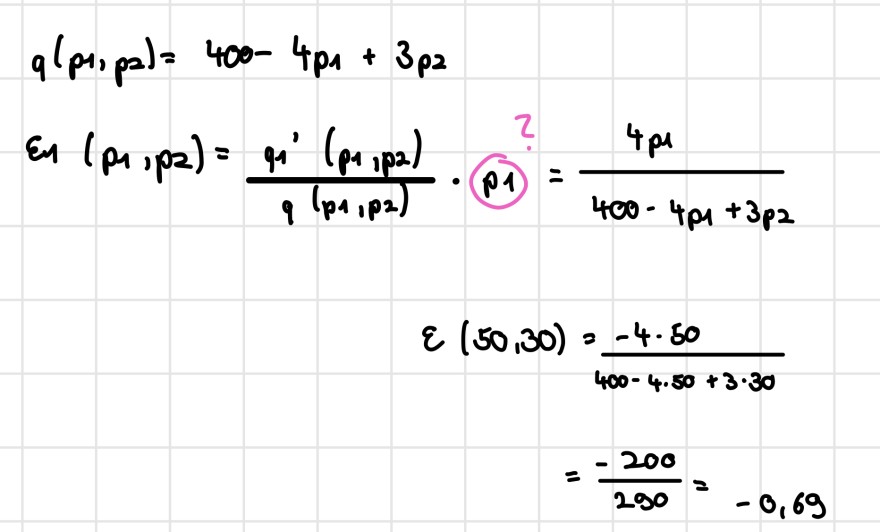
Text erkannt:
\( \begin{aligned} q\left(p_{1}, p_{2}\right)=400-4 p_{1}+3 p_{2} \\ \varepsilon_{1}\left(p_{1}, p_{2}\right)=\frac{q_{1}\left(p_{11}, p_{2}\right)}{q\left(p_{1}, p_{2}\right)} \cdot p_{p 1}=\frac{4 p \mu}{400-4 p 1+3 p_{2}} \\ \varepsilon(50,30)=\frac{-4 \cdot 50}{400-4 \cdot 80+3 \cdot 30} \\ &=\frac{-200}{290}=-0,69 \end{aligned} \)
So ist es richtig aufgeschrieben :) es ist immer -4p1, der Text erkennt nur manchmal meine Schrift nicht haha