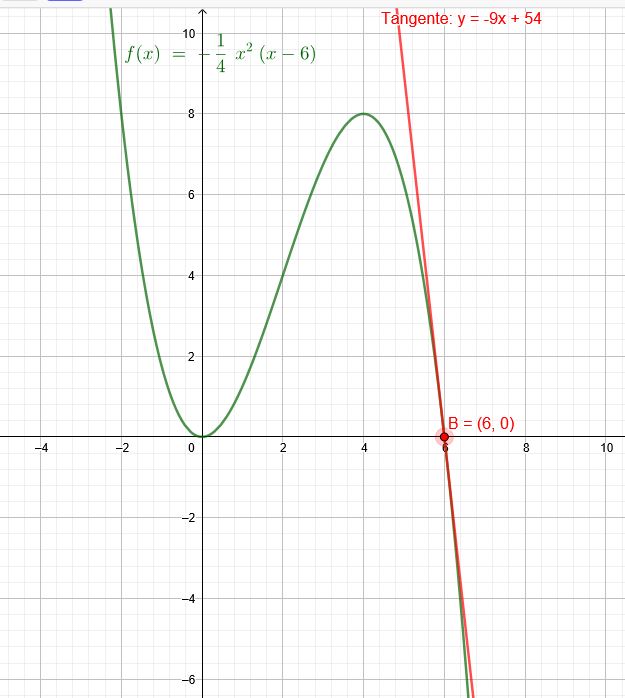
"Der Funktionsgraph einer ganzrationalen Funktion 3. Grades schneidet die x-Achse bei
\(x₁ = 0\) und \(x₂ = 6\). An der linken Nullstelle befindet sich ein Tiefpunkt der Funktion. An der
rechten Nullstelle kann eine Tangente mit der Steigung −9 angelegt werden.
Bestimme die Gleichung der Funktion."
schneidet die x-Achse bei \(x₁ = 0\) (und Tiefpunkt doppelte Nullstelle) und \(x₂ = 6\):
\(f(x)=a*x^2*(x-6)\)
rechten Nullstelle Tangente mit der Steigung −9:
\(f´(x)=2*a*x*(x-6)+a*x^2*1\)
\(f´(6)=2*a*6*(6-6)+a*6^2=36a=-9\) →\(a=-\frac{1}{4}\)
\(f(x)=-\frac{1}{4}*x^2*(x-6)\)