Aufgabe:
Im Spiel 'Mini-Tetris' geht es darum, ein \( 2 \times n \) Rechteck mit den folgenden Bausteinen lückenlos und ohne Überlappungen zu belegen:
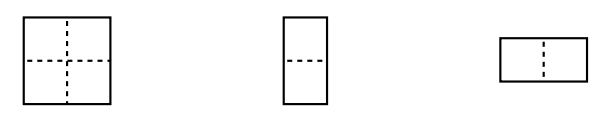
Es sei \( T_{n} \) die Anzahl der verschiedenen Möglichkeiten, mit diesen Bausteinen ein \( 2 \times n \) Rechteck so zu belegen.
Bestimmen Sie \( T_{1} \) und \( T_{2} \), finden Sie eine Formel für \( T_{n} \) für \( n \geq 3 \) als Funktion von \( T_{n-1} \) und \( T_{n-2} \), und beweisen Sie durch starke Induktion, dass
\(T_{n}=\frac{1}{3}\left[2^{n+1}+(-1)^{n}\right] \)
ist.