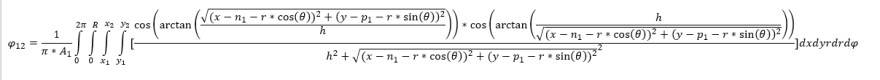Aufgabe:
Lösung eines komplizierten Integrals.
Problem/Ansatz:
Um den Sichtfaktor zwischen einer Kreis- und einer Rechteckfläche zu berechnen ist bei mir hier aus der Grundformel ein ziemlich kompliziertes Integral entstanden, welches ich nicht zu lösen bekomme. n und p sind dabei feste Koordinaten im x-y-Koordinatensystem und h die Entfernung der Flächen. Ich habe mittlerweile echt vieles ausprobiert, komme aber auf keine Lösung. Wäre für Hilfe, einen Ansatz oder eine Idee wirklich sehr dankbar!! Liebe Grüße Jonathan
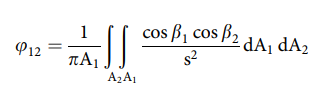
Text erkannt:
\( \varphi_{12}=\frac{1}{\pi \mathrm{A}_{1}} \iint_{\mathrm{A}_{2} \mathrm{~A}_{1}} \frac{\cos \beta_{1} \cos \beta_{2}}{\mathrm{~s}^{2}} \mathrm{dA}_{1} \mathrm{dA}_{2} \)