Population von Fruchtfliegen (Drosophila)

Question

Um 1920 stellte R. Pearl experimentell fest, dass die Änderungsrate dP/dt einer Population von Fruchtfliegen (Drosophila) mit der Populationsgröße über die Gleichung

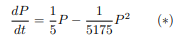
verbunden ist, wobei hier t in Tagen gemessen wird. Die eindeutige Lösung dieser Differentialgleichung zur Anfangsbedingung P(0) = 2 ist gegeben durch

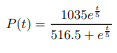
(a) Zeigen Sie, dass die Funktion

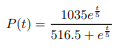eine Lösung der obigen Differentialgleichung (∗) zur Anfangsbedingung P(0) = 2 ist.

b) Zeigen Sie, dass die Population der Fruchtfliegen ständig wächst, aber niemals mehr als 1035 Mitglieder hat.

c) Bei welcher Populationsgröße und an welchem Tag beginnt die Wachstumsrate abzunehmen?

Frage: Wie und mit welchen Verfahren gehe ich folgende Aufgaben an? Würde mich um mögliche Lösungswege freuen

Answer 1

a) Du musst zeigen, dass die Differentialgleichung erfüllt ist und das P(0) = 2 gilt.

$$ \frac{\partial}{\partial t} \frac{1035 e^{t / 5}}{516.5+e^{t / 5}}=\frac{1}{5} \times \frac{1035 e^{t / 5}}{516.5+e^{t / 5}}-\frac{1}{5175}\left(\frac{1035 e^{t / 5}}{516.5+e^{t / 5}}\right)^{2} $$

Schaffst du es p(t) abzuleiten und umzuformen?

Comments

Ich denke schon, bzw ich hoffe dass das hier so korrekt ist. Und was folgt jetzt?

---

Meine Gleichung hatte 2 Seiten. Du hast jetzt die Linke Seite berechnet. Jetzt müsstest du die rechte Seite berechnen und zeigen, dass exakt dasselbe herauskommt.

---

Ich kriege hier irgendwie was anderes raus als vorher:

---

Da deine Ableitung richtig war, gehe ich davon aus, dass du die rechte Seite nicht genug zusammengefasst hast.

Wolframalpha sagt da kommt das gleiche heraus:

---

Alles klar vielen Dank für die Hilfe. Wie man bei Aufgabe b) und c) verfahren soll wüssten sie nicht auch noch zufällig?

---

b)

Ein Wachstum kannst du zeigen

P(t + x) ≥ P(t) mit x > 0 oder auch P'(t) ≥ 0

Die Obergrenze kannst du zeigen

P(t) ≤ 1035

c)

Wendepunkt

P''(t) = 0