Aufgabe:
Skisprungschanze in Garmisch Patenkirchen:
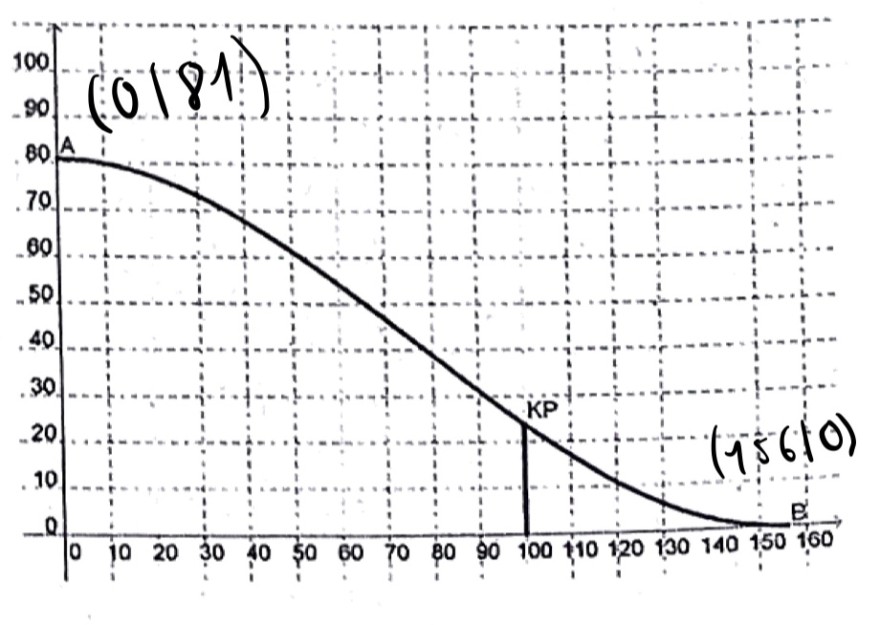
Der Aufsprunghügel der großen Olympia-Schanze in Garmisch Patenkirchen hat etwa das in der Abbildung erkennbare Profil. Für die markierten Punkte A und B gilt dabei: A liegt 81m höher als B. Die waagerechte Entfernung zwischen den beiden Punkten besteht rund 156m.
a) Bestimmen sie eine ganzrationale Funktion 3. Grades, die das Profil des Aufsprunghügels im Bereich von A bis B näherungsweise beschreibt. Hinweis: Die Steigung des Aufsprunghügels in den Punkten A und B werde modellhaft vereinfachend als null angenommen. (Kontrollergebniss: f(x)= 162/3796416x^3 - 27/2704x^2 +81)
b) Berechnen sie den Punkt, indem die Schanze am steilsten ist.
Problem/Ansatz:
Hallo zusammen, ich komme einfach nicht auf die richtige Lösung. Ich habe zuerst:
f(x)=ax^3+bx^2+cx+d
f‘(x)=3ax^2+2bx+c
f‘‘(x)= 6ax+2b
aufgestellt
Dann die Bedingungen aufgestellt:
1: f(0)= 81
2: f(156)= 0
3: f‘(0)= 0
4: f‘(156)= 0
Dann eingesetzt:
a(0)^3+ b(0)^2+c(0)+d=81
a(156)^3+b(156)^2+c(156)+d= 0
3a(0)^2+2b(0)+c= 0
3a(156)^2+2b(156)+c=0
Daraus ergibt sich ja dann:
d= 81
156^3a+ 156^2b+81=0
c=0
73008a+ 312b=0
= a: 9/1282112 b: -81/49312
Da kommen dann allerdings falsche Werte raus, bzw nicht die aus dem Kontrollergebniss…
Danke schonmal im Voraus!