Aufgabe:
Zeigen Sie, dass die nachstehenden Abbildungen bijektiv sind und geben Sie die Umkehrabbildung an.
(i) f: [0,∞) -> [0,1), f(x) = x/(x+1)
(ii) v: [0,∞) -> [0,B), g(S) = BS/(S+K) , wobei B,K ∈ ℝ>0 Konstanten sind.
Nun habe ich bei (i) schon die Injektivität gezeigt, frage mich aber, wie genau man die Surjektivität zeigt.
Nach meinem Verständnis läuft die Funktion gegen 1, wird aber nie genau 1. Wäre damit dann nicht die Surjektivität widerlegt? (Wenn ja, wie kann man das schriftlich belegen?)
Zu den Umkehrabbildungen muss ich mich selber auch noch genauer informieren und bei (ii) weiß ich noch garnicht wirklich, wie ich anfangen soll. Ich habe grundsätzlich auch nur Infos gefunden, wie man solche Aufgaben löst, wenn der Bildbereich alle reellen Zahlen oder alle positiven reellen Zahlen beinhaltet, nicht aber wenn er anderweitig eingeschränkt ist, wie hier.
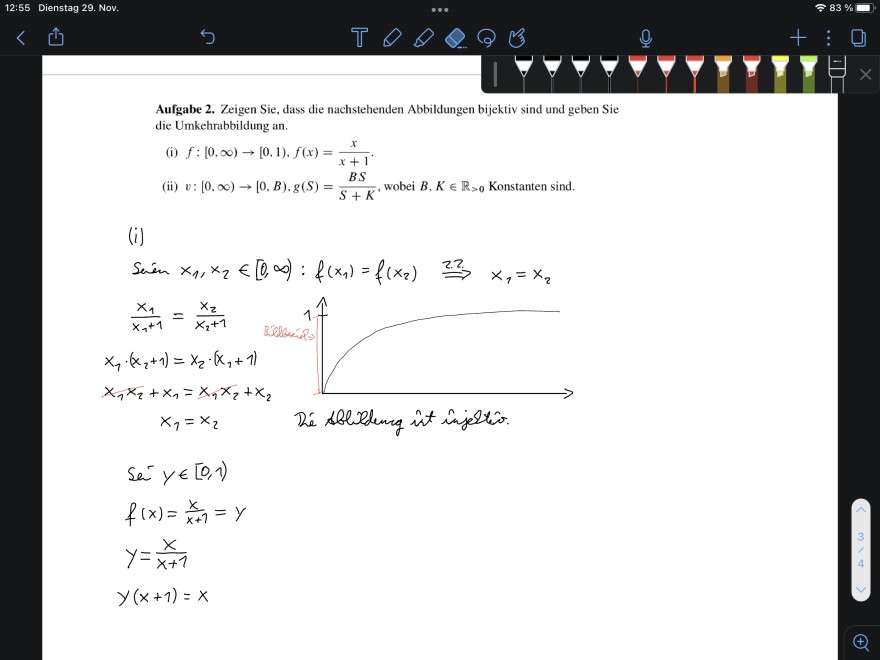
Text erkannt:
12:55 Dienstag 29. Nov.
Aufgabe 2. Zeigen Sie, dass die nachstehenden Abbildungen bijektiv sind und geben Sie die Umkehrabbildung an.
(i) \( f:[0, \infty) \rightarrow[0,1), f(x)=\frac{x}{x+1} \).
(ii) \( v:[0, \infty) \rightarrow[0, B), g(S)=\frac{B S}{S+K} \), wobei \( B, K \in \mathbb{R}_{>0} \) Konstanten sind.
(i)
Seien \( x_{1}, x_{2} \in[0, \infty): f\left(x_{1}\right)=f\left(x_{2}\right) \stackrel{2.2}{\Longrightarrow} x_{1}=x_{2} \)
\( \frac{x_{1}}{x_{1}+1}=\frac{x_{2}}{x_{2}+1} \)
\( x_{1} \cdot\left(x_{2}+1\right)=x_{2} \cdot\left(x_{1}+1\right) \)
\( x_{1} x_{2}+x_{1}=x_{1} x_{2}+x_{2} \)
\( x_{1}=x_{2} \)
ser \( y \in[0,1) \)
\( f(x)=\frac{x}{x+1}=y \)
\( y=\frac{x}{x+1} \)
\( y(x+1)=x \)
Problem/Ansatz:
Sei y ∈ [0,1)
f (x) = x/(x+1) = y
y = x/(x+1)
x = (x+1)