Könnte man bei a einfach separieren?

Question

Aufgabe: DGL lösen

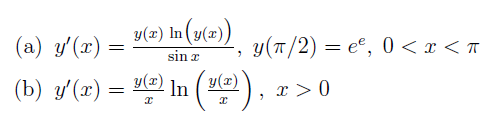
Text erkannt:

(a) $y^{\prime}(x)=\frac{y(x) \ln (y(x))}{\sin x}, y(\pi / 2)=e^{e}, 0<x<\pi$
(b) $y^{\prime}(x)=\frac{y(x)}{x} \ln \left(\frac{y(x)}{x}\right), x>0$

Problem/Ansatz: Ich bin im Lösen von DGLs noch nicht so sicher. Könnte man bei a einfach separieren? Und müsste man dann die Anfangswerte als obere oder untere grenze des integrals einsetzen?

Answer 1

Hallo,

Könnte man bei a einfach separieren? Und müsste man dann die Anfangswerte als obere oder untere Grenze des Integrals einsetzen? JA

b) Lösung durch Substitution

z=y/x

y=z *x

y'=z+z' x

Comments

Ok, danke dir