Aufgabe:
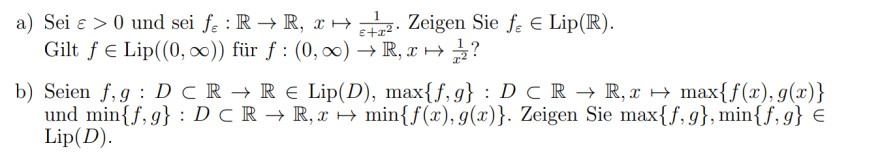
Text erkannt:
a) Sei \( \varepsilon>0 \) und sei \( f_{\varepsilon}: \mathbb{R} \rightarrow \mathbb{R}, x \mapsto \frac{1}{\varepsilon+x^{2}} \). Zeigen Sie \( f_{\varepsilon} \in \operatorname{Lip}(\mathbb{R}) \).
Gilt \( f \in \operatorname{Lip}((0, \infty)) \) für \( f:(0, \infty) \rightarrow \mathbb{R}, x \mapsto \frac{1}{x^{2}} \) ?
b) Seien \( f, g: D \subset \mathbb{R} \rightarrow \mathbb{R} \in \operatorname{Lip}(D), \max \{f, g\}: D \subset \mathbb{R} \rightarrow \mathbb{R}, x \mapsto \max \{f(x), g(x)\} \) und \( \min \{f, g\}: D \subset \mathbb{R} \rightarrow \mathbb{R}, x \mapsto \min \{f(x), g(x)\} \). Zeigen Sie \( \max \{f, g\}, \min \{f, g\} \in \) \( \operatorname{Lip}(D) \)
Problem:
Leider komme ich nicht mit Ungleichungen klar. Das Einsetzen in die Lipschitz-Formel schaffe ich, allerdings nicht mehr die Umformung.
Brauche Hilfe beim Lösen von a und b.
Danke für Eure Hilfe!
Viele Grüße