Wie kann ich den Umfangswinkelsatz (Peripheriewinkelsatz) beweisen?

Question

wie kann ich den Umfangswinkelsatz beweisen?

Präzision aus Kommentar: wenn in einem kreis ein mittelpunkt und am aussenkreis drei punkte und die werden miteinander verbunden. dann entsteht in der mitte ein winkel und die winkel am aussenkreis sind die hälfte kleiner.

Anhand eines Satzes oder auch einer Aufgabe?

Ich habe es gezeichnet ,aber wie kann ich es beweisen.

Comments

Könntest du bitte noch angeben, was dieser Satz denn genau behauptet?

---

wennin einem kreis ein mittelpunkt und am aussenkreis drei punkte und die werden miteinander verbunden.

dann entsteht in der mitte ein winkel und die winkel am aussenkreis sind die hälfte kleiner.

warum?

---

Aha. Das wird bei uns Peripheriewinkelsatz genannt.

---

Ich hoffe, du kannst damit etwas anfangen: http://www.math.uni-bremen.de/didaktik/ma/ralbers/Veranstaltungen/Aarchiv/GeoPeitg09/Material/Protokoll_090507_SehnenSek.pdf

---

danke ,das hatte ich auch schon gefunden,aber gibt es ein merksatz oder eine genaue beschreibung,warum das so ist?

Answer 1

Hier mal ein Beweis für den Fall, dass der Umkreismittelpunkt im Innern des Dreiecks liegt. Du kannst nötigenfalls noch andere Fälle entsprechend beweisen.

Answer 2

Zunächst eine ganz so schöne Skizze:

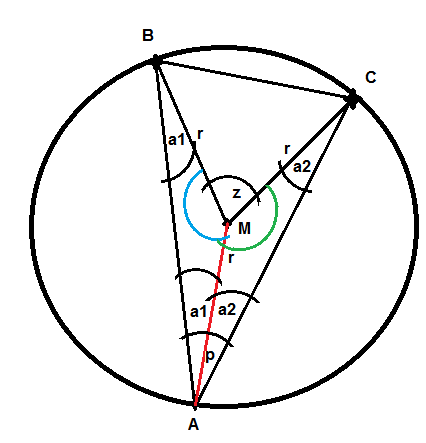
Die Behauptung des Peripheriewinkelsatzes lautet:

 

Für den Peripheriewinkel p und den Zentriwinkel z gilt die Beziehung:

 z =  2 *  p

 

Zeigen lässt sich das z.B. so:

Zeichnet man die Strecke AM ein (rot), so teilt diese den Winkel p in zwei Teilwinkel a1 und a2

DA MA, MB und MC Radien des Kreises sind, sind die Dreiecke AMB und AMC gleichschenklige Dreiecke mit den Basiswinkeln a1 bzw. a2

Also gilt für den Scheitelwinkel des Dreiecks AMB (blau):

AMB = 180 ° - 2 a1

und für den Scheitelwinkel des Dreiecks AMC (grün):

AMC = 180° - 2 a2

Daraus folgt für den Zentriwinkel z:

z = 360 ° - AMB - AMC

= 360 ° - ( 180 ° - 2 a1 ) - ( 180 ° - 2 a2 )

= 2 a1 + 2 a2

= 2 ( a1 + a2 )

= 2 * p