Aufgabe:
Zeigen Sie, dass h'(t) = F(h(t))h(t), wobei F(h) = F(h(t)) = α ln (k/h(t))
die Vermehrungsrate beschreibt.
Ich lade die Aufgabe ganze Aufgabe als Datei hoch, da es so übersichtlicher ist, als würde ich hier alles schreiben.
Die Teilaufgabe (i) habe ich hinbekommen, bei (ii) komme ich aber nicht weiter. Ich habe die Ableitung gebildet (hoffentlich richtig), und lade den Ansatz dazu auch noch hoch. Vermutlich habe ich aber falsch abgeleitet, oder mir fehlen die Kenntnisse, um die Ableitung so umzuformen, dass sie das gleiche aussagt, wie F(h(t))h(t).

Text erkannt:
Aufgabe 3. Mit der Gompertz-Funktion
\( h(t)=k e^{\ln \left(\frac{h_{0}}{k}\right) e^{-\alpha t}} \)
lässt sich näherungsweise die Größe \( h(t) \) eines Tumors in Abhängigkeit von der Zeit \( t \) darstellen. Hierbei ist \( \alpha \) eine positive Konstante, \( h_{0} \) die Größe des Tumors zu Beobachtungsbeginn \( (t=0) \) und \( k \) die Sättigungsgrenze, d. h. die maximale Größe, die der Tumor aufgrund der vorhandenen Gegebenheiten erreichen kann.
(i) Bestimmen Sie \( \lim \limits_{t \rightarrow \infty} h(t) \).
(ii) Zeigen Sie, dass \( h^{\prime}(t)=F(h(t)) h(t) \), wobei
\( F(h)=F(h(t))=\alpha \ln \left(\frac{k}{h(t)}\right) \)
die Vermehrungsrate beschreibt.
(iii) Bestimmen Sie \( \lim \limits_{h \rightarrow 0^{+}} F(h) \) und interpretieren Sie das Ergebnis.
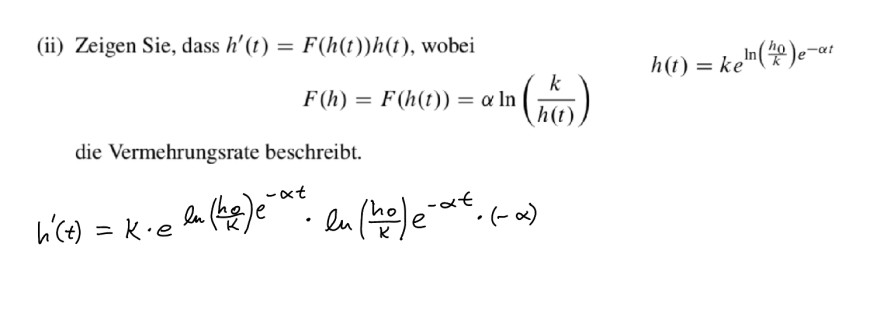
Text erkannt:
(ii) Zeigen Sie, dass \( h^{\prime}(t)=F(h(t)) h(t) \), wobei
\( F(h)=F(h(t))=\alpha \ln \left(\frac{k}{h(t)}\right) \)
\( h(t)=k e^{\ln \left(\frac{h_{0}}{k}\right) e^{-\alpha t}} \)
die Vermehrungsrate beschreibt.