Aufgabe:
Injektivität, surjektivität, bihektivität beweisen
Problem/Ansatz:
Hallo alle zusammen,
Meine Aufgabenstellung lautet wie folgt:
Prüfen Sie, welche der folgenden Audrücke Funktionen f: (-1,1) ->(-1,1) definieren und ob diese injektiv, surjektiv oder bijektiv ist.
Folgende Audrücke sind gegeben:
F(x)=x-x2 F(x)=x^2+x/2
Nun weiß ich nicht wie ich vorgehen soll und bräuchte sehr dringend 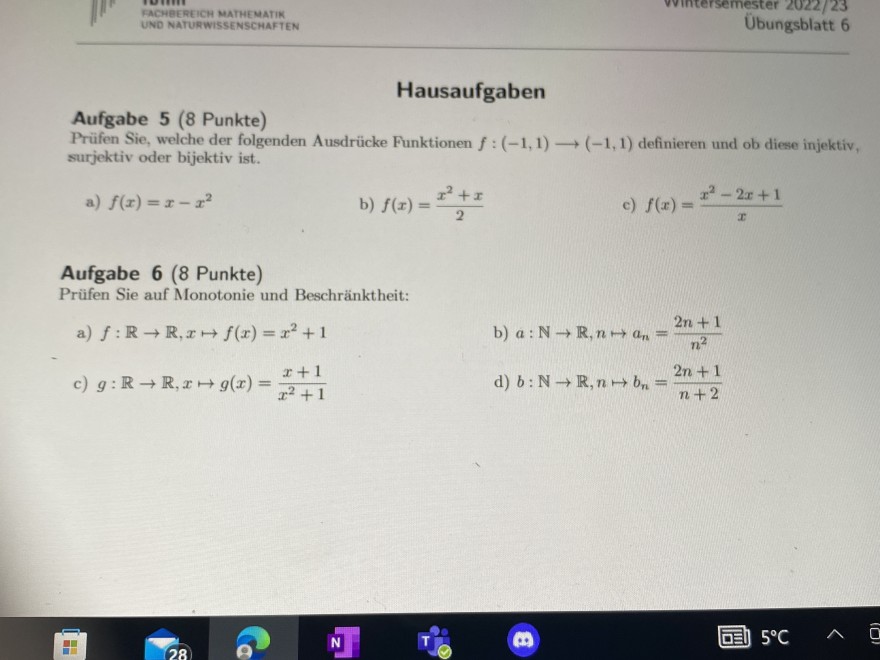
Text erkannt:
FACHEEREICH MATHEMATIK
UND NATURWISSENSCMAFTEN
Übungsblatt 6
Hausaufgaben
Aufgabe 5 (8 Punkte)
Prüfen Sie, welche der folgenden Ausdrücke Funktionen \( f:(-1,1) \longrightarrow(-1,1) \) definieren und ob diese injektiv, surjektiv oder bijektiv ist.
a) \( f(x)=x-x^{2} \)
b) \( f(x)=\frac{x^{2}+x}{2} \)
c) \( f(x)=\frac{x^{2}-2 x+1}{x} \)
Aufgabe 6 (8 Punkte)
Prüfen Sie auf Monotonie und Beschränktheit:
a) \( f: \mathbb{R} \rightarrow \mathbb{R}, x \mapsto f(x)=x^{2}+1 \)
b) \( a: \mathbb{N} \rightarrow \mathbb{R}, n \rightarrow a_{n}=\frac{2 n+1}{n^{2}} \)
c) \( g: \mathbb{R} \rightarrow \mathbb{R}, x \mapsto g(x)=\frac{x+1}{x^{2}+1} \)
d) \( b: \mathbb{N} \rightarrow \mathbb{R}, n \mapsto b_{n}=\frac{2 n+1}{n+2} \)
Text erkannt:
\( \times \mid \text { fn wS22/23 Mathematik 1 BTC: Öb } \times \text { Wof WS2022 Mathe } 1 \text { Blatt } 6 \text { (1).p } \)
\( \text { . }-+\infty \text { \& }+\text { \& }\left[A \mid A^{n}\right. \)
h_da
Hausaufgaben
Aufgabe 5 ( 8 Punkte)
Prüfen Sie, welche der folgenden Ausdrücke Funktionen \( f:(-1,1) \longrightarrow(-1,1) \) definieren und ob diese injektiv, surjektiv oder bijektiv ist.
a) \( f(x)=x-x^{2} \)
b) \( f(x)=\frac{x^{2}+x}{2} \)
c) \( f(x)=\frac{x^{2}-2 x+1}{x} \)
Aufgabe 6 (8 Punkte)
Prüfen Sie auf Monotonie und Beschränktheit: