Aufgabe:
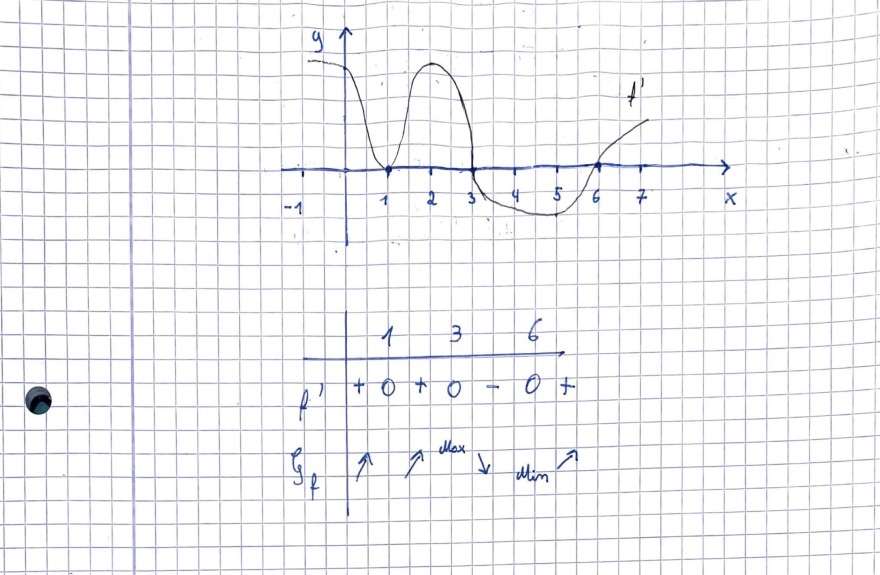
Gegen ist der Graph der Ableitung einer Funktion. Welche Aussagen sind wahr? Erkläre.
(a) f(2) ≥ f(3)
(b) f(4) ≤ 0
(c) f erreicht ein lokales Minimum in 1
(d) f erreicht ein lokales Maximum in 3
(e) f erreicht ein lokales Minimum in 6
(f) f(4) - f(3) ≥ f(5) - f(4)
Problem/Ansatz:
(a) Falsch: Da f(3) ein lokales Maximum ist (siehe Zeichentabelle)
(b) Hier bräuchte ich Hilfe: Ich weiss, dass die Funktion hier zwar fallend ist, aber woher soll ich wissen, dass sie ≤ 0 ist?
(c) Falsch: Ableitung ist zwar 0 in 1, aber es ist keine Extremstelle, da sie vor und nach 1 steigend ist (siehe Zeichentabelle).
(d) Wahr: Ableitung ist 0 und Funktion geht von steigend zu fallend (siehe Zeichentabelle)
(e) Wahr: Ableitung ist 0 und Funktion geht von fallend zu steigend (siehe Zeichentabelle)
(f) Hier weiss ich leider auch nicht weiter. Muss ich hier Lagrange oder Rolle anwenden?