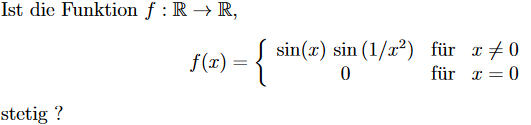
Text erkannt:
Ist die Funktion \( f: \mathbb{R} \rightarrow \mathbb{R} \),
\( f(x)=\left\{\begin{array}{cll} \sin (x) \sin \left(1 / x^{2}\right) & \text { für } & x \neq 0 \\ 0 & \text { für } & x=0 \end{array}\right. \)
stetig ?
Beweis: Für x∈R /{0} ist f(x) als Zusammensetzung steiger Funktionen wieder stetig. Betrachtet man jetzt x=0. Somit folgt aus (sin(x)^2+cos(x)^2=1
(sin(x)^2=1-(cos(x)^2 ⇒|sin(x)≤1
Also gilt: |f(x)-f(0)| = |sin(x)*sin(1/x^2)|<=|x|
Für eine beliebige Folge (x_n) mit x_n--->0 folgt
limx_n-->0 |f(x_n)-f(0)| ≤ limx_n--->0 |x_n|=0
und somit auch f(x_n) -->f(0). Also ist f auf ganz R stetig
Ist das richtig oder ist etwas falsch?
