Aufgabe:
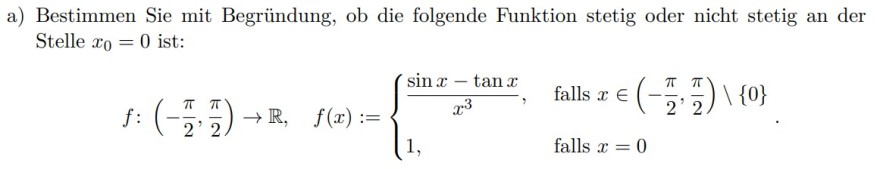
Text erkannt:
a) Bestimmen Sie mit Begründung, ob die folgende Funktion stetig oder nicht stetig an der Stelle \( x_{0}=0 \) ist:
\( f:\left(-\frac{\pi}{2}, \frac{\pi}{2}\right) \rightarrow \mathbb{R}, \quad f(x):=\left\{\begin{array}{ll} \frac{\sin x-\tan x}{x^{3}}, & \text { falls } x \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right) \backslash\{0\} \\ 1, & \text { falls } x=0 \end{array}\right. \)
Problem/Ansatz:
Benötige bitte einen Lösungsweg, komme alleine nicht weiter :(