
Text erkannt:
Gegeben seien drei Basen \( \mathcal{B}, \mathcal{C}, \mathcal{D} \) von \( \mathbb{R}^{2} \) sowie ein Vektor \( v \in \mathbb{R}^{2} \)
\( \begin{array}{l} \mathcal{B}=\left\{b_{1}=\left(\begin{array}{l} 1 \\ 1 \end{array}\right), \quad b_{2}=\left(\begin{array}{l} 2 \\ 1 \end{array}\right)\right\}, \quad \mathcal{C}=\left\{c_{1}=\left(\begin{array}{c} 2 \\ -1 \end{array}\right), \quad c_{2}=\left(\begin{array}{l} 4 \\ 3 \end{array}\right)\right\}, \\ \mathcal{D}=\left\{d_{1}=\left(\begin{array}{l} 1 \\ 2 \end{array}\right), \quad d_{2}=\left(\begin{array}{l} 2 \\ 3 \end{array}\right)\right\}, \quad v=\left(\begin{array}{l} 2 \\ 5 \end{array}\right) . \\ \end{array} \)
Sei \( f: \mathbb{R}^{2} \longrightarrow \mathbb{R}^{2} \) die linear Abbildung gegeben durch \( f\left(c_{1}\right)=d_{1}, f\left(c_{2}\right)=d_{2} \).
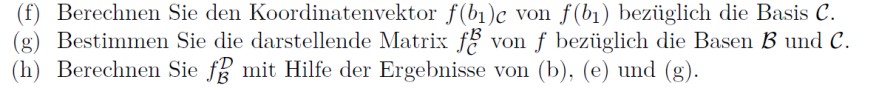
Text erkannt:
(f) Berechnen Sie den Koordinatenvektor \( f\left(b_{1}\right) \mathcal{C} \) von \( f\left(b_{1}\right) \) bezüglich die Basis \( \mathcal{C} \).
(g) Bestimmen Sie die darstellende Matrix \( f_{\mathcal{C}}^{\mathcal{B}} \) von \( f \) bezüglich die Basen \( \mathcal{B} \) und \( \mathcal{C} \).
(h) Berechnen Sie \( f_{\mathcal{B}}^{\mathcal{D}} \) mit Hilfe der Ergebnisse von (b), (e) und (g).
Aufgabe: