Aufgabe:
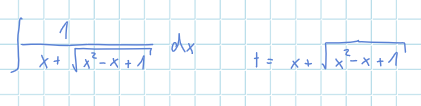
Text erkannt:
\( \int \frac{1}{x+\sqrt{x^{2}-x+1}} d x \quad t=x+\sqrt{x^{2}-x+1} \)
Man soll folgendes Integral mit HIlfe der angegebenen Substitution lösen.
Problem/Ansatz:
Als Hinweis sind die Substitution gegeben und das man dannach noch Parzialbruchzerlegung machen soll.
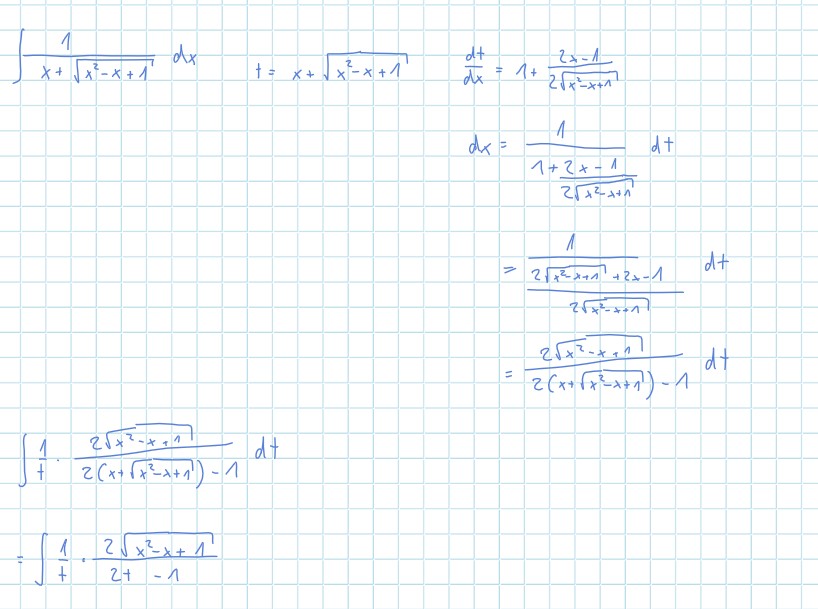
Text erkannt:
\( \int \frac{1}{x+\sqrt{x^{2}-x+1}} d x \quad t=x+\sqrt{x^{2}-x+1} \quad \frac{d t}{d x}=1+\frac{2 x-1}{2 \sqrt{x^{2}-x+1}} \)
\( =\frac{1}{\frac{2 \sqrt{x^{2}-x+1}+2 x-1}{2 \sqrt{x^{2}-x+1}}} d t \)
\( =\frac{2 \sqrt{x^{2}}-x+1}{2\left(x+\sqrt{x^{2}-x+1}\right)-1} d t \)
\( \int \frac{1}{t} \cdot \frac{2 \sqrt{x^{2}-x+1}}{2\left(x+\sqrt{x^{2}-x+1}\right)-1} d t \)
\( =\int \frac{1}{t} \cdot \frac{2 \sqrt{x^{2}-x+1}}{2+-1} \)
Das kommt bei mir bei der substitution raus, das kann doch aber nicht sein oder? Weil so wäre ja im Intergral der Term noch von x abhängig, obwohl ich das substituieren wollte.
Kann mir da jemand weiter helfen? Würde mich über jede Hilfe freuen :)