Untervektorräume eines Vektorraums bestimmen, Abbildungen auf Linearität untersuchen

Question

Aufgabe:

a) Entscheiden Sie, welche der folgenden Mengen U Untervektorräume des entsprechenden
K-Vektorraums V sind:

(i) K = R, V = R3, U = {(x, y, z) ∈ R3 | x2 + y2 = z}
(ii) K = R, V = R3, U = {(x, y, z) ∈ R3 | x + y = z}

Sei n ∈ N.

Text erkannt:

(iii) \( K=\mathbb{Z}_{2}, \quad V=\mathbb{Z}_{2}^{2 n} \), \( U=\left\{\left(x_{1}, \ldots, x_{2 n}\right) \in \mathbb{Z}_{2}^{2 n} \mid\left(x_{1}, \ldots, x_{2 n}\right)\right. \) enthält eine gerade Anzahl \( \overline{1} \)-en \( \} \);
(iv) \( K=\mathbb{Z}_{2}, \quad V=\mathbb{Z}_{2}^{2 n} \),
\( U=\left\{\left(x_{1}, \ldots, x_{2 n}\right) \in \mathbb{Z}_{2}^{2 n} \mid\left(x_{1}, \ldots, x_{2 n}\right)\right. \) enthält eine ungerade Anzahl \( \overline{1} \)-en \( \} \).

b) Untersuchen Sie die folgenden Abbildungen auf Linearität:

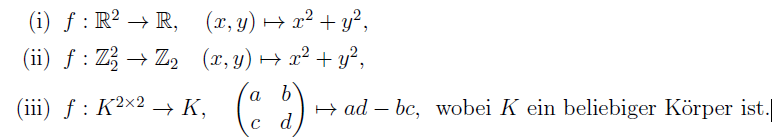
Problem/Ansatz:

Hey Leute ich komme leider mit dieser Aufgabe nicht zurecht und würde mich über Hilfe echt freuen. Das Thema liegt mir leider überhaupt nicht und egal wie viele Videos ich mir dazu anschaue, ich werde einfach nicht schlau daraus.

Answer 1

Bei i) wären z.B. die Tripel (2;2;8) und (3;3;18) in U.

Deren Summe aber nicht, also kein Unterraum von ℝ^3.

Bei i) ist die Summe von zweien allerdings auch wieder darin;

denn wenn (a,b,c) und (x,y,z) in U sind, dann gilt

ja a+b=c und x+y=z .

Daraus folgt aber  (a+x)+(b+y)=c+z , also

(a+x, b+y,c+z) auch in U. Und für (x,y,z) in U

ist auch c* (x,y,z) in U für alle c∈ℝ.

Answer 2

Zu (a) (iii):

\(U\) ist der Kern der linearen Abbildung

\((x_1,\cdots, x_{2n}) \mapsto x_1+\cdots + x_{2n}\).

Zu (b)(ii):

In \(Z_2\) gilt \(x^2=x\; \forall x \in Z_2\). Damit wird die Sache

schön einfach.