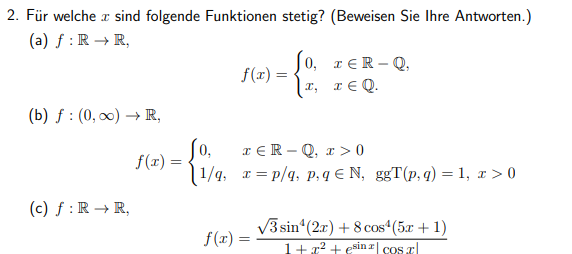
Text erkannt:
2. Für welche \( x \) sind folgende Funktionen stetig? (Beweisen Sie Ihre Antworten.)
(a) \( f: \mathbb{R} \rightarrow \mathbb{R} \),
\( f(x)=\left\{\begin{array}{ll} 0, & x \in \mathbb{R}-\mathbb{Q}, \\ x, & x \in \mathbb{Q} . \end{array}\right. \)
(b) \( f:(0, \infty) \rightarrow \mathbb{R} \),
(c) \( f: \mathbb{R} \rightarrow \mathbb{R} \),
\( f(x)=\frac{\sqrt{3} \sin ^{4}(2 x)+8 \cos ^{4}(5 x+1)}{1+x^{2}+e^{\sin x}|\cos x|} \)
ich brauch bitte bitte Hilfe.
Es gibt wie ihr ja wisst verschiedene Arten um die Stetigkeit zu beweisen und ich verstehe was da steht, ich kenne auch die Differenzierbarkeit, aber ich habe gaaar keine Ahnung von allem ab und bei der a), b) ist genau so schlimm, die c) sieht aber machbar aus.
Kann mir bitte jemand zeigen, wie man die Stetigkeit beweist, denn durch epsilon delta oder den folgenkriterium bekomme ich es nicht hin.